Week1 - Motivation and Basics

in Mathematics / Machine learning

Table of Contents

  1. Maximum Likelihood Estimation
    1. Binomial Distribution
    2. Maximum Likelihood Estimation
    3. MLE calculation
    4. Number of Trials & Simple Error Bound
  2. Maximum a Posteriori Estimation
    1. Incorporating Prior Knowledge
    2. More Formula from Bayes Viewpoint
    3. Maximum a Posterior Estimation
    4. Conclusion from Anecdote
  3. Basics
    1. Probability
    2. Conditional Probability
    3. Probability Distribution
    4. Normal Distribution
    5. Beta Distribution
    6. Binomial Distribution
    7. Multinomial Distribution
  4. Summary
  • Weekly Objectives
    • Motivate the study on
      • Machinelearning,AI,Datamining….
      • Why? What?
      • Overview of the field
    • Short questions and answers on a story
      • What consists of machine learning?
      • MLE
      • MAP
    • Some basics
      • Probability
      • Distribution
      • And some rules…

Maximum Likelihood Estimation

Binomial Distribution

  • Binomialdistributionis
    • The discrete probability distribution
    • Of the number of successes in a sequence of n independent yes/no experiments, and each success has the probability of \(\theta\)
    • Also called a Bernoull iexperiment
  • Flips are i.i.d
    • Independent events (처음 던질 때와 두 번째 던질 때 연관이 없는 상태)
    • Identically distributed according to binomial distribution (던질때마다 동일한 확률 분포를 가질 때)
  • P(H) = \(\theta\), P(T)=1 - \(\theta\)
  • P(HHTHT)= \(\theta \cdot \theta \cdot (1- \theta) \cdot \theta \cdot (1- \theta) = \theta ^3(1 - \theta)^2\)
  • Let’s say
    • D as Data = H, H, T, H, T
      • n = 5
      • k = \(a_H\) =3
      • p = \(\theta\)
    • p(D\(\mid \theta\)) = \(\theta ^{a_H} (1-\theta)^{a_T}\)

How to get the probability?

Maximum Likelihood Estimation

  • p(D\(\mid \theta\)) = \(\theta ^{a_H} (1-\theta)^{a_T}\)
    • Data: We have obseved the sequence data of D with \(a_H\) and \(a_T\)
  • Our hypothesis:
    • The gambiling result follows the binomial distribution of \(\theta\)
  • How to make our hypothesis strong(어떻게 ‘참’이다라고 말할 수 있을까)?
    • Finding out a better distribution of the observation
      • Can be done, but you need more rational.
      • Binomial distribution보다 좋은 hypothesis 구조가 있다면, 이것도 가능하지만 더 많은 합리적 생각이 필요.
    • Finding out the best candidate of \(\theta\)
      • What’s the condition to make \(\theta\) most plausible ?
      • \(\theta\)를 최적화하여 hypothesis를 strong하게 만들 수 있음.

어떤 \(\theta\)를 선택했을 때 data를 가장 잘 설명할 수 있을까?

  • One candidate is the __Maximum Likelihood Estimation (MLE) of \(\theta\)
    • Choose \(\theta\) that maximized the probability of obseverd data
\[\begin{aligned} \hat{\theta} = argmax_\theta P(D| \theta) \end{aligned}\]

MLE calculation

  • \[\hat{\theta} = argmax_\theta P(D| \theta) = argmax_\theta \theta ^{a_H} (1-\theta)^{a_T}\]
  • This is going nowhere, so you use a trick (자승을 처리하기 까다로움)
    • Using the log function.
  • \[\hat{\theta} = argmax_\theta ln P(D| \theta) = argmax_\theta ln(\theta ^{a_H} (1-\theta)^{a_T}) = argmax_\theta ( a_H ln\theta + a_T ln (1-\theta) )\]
  • Then, thish is a maximization problem, so you use a derivative that is set to zero
    • \[\frac{d}{d\theta} ( a_H ln\theta + a_T ln (1-\theta) ) = 0\]
    • \[\frac{a_H}{\theta} - \frac{a_T}{1-\theta} = 0\]
    • \[\theta = \frac{a_H}{a_T + a_H}\]
    • When \(\theta\) is \(\frac{a_H}{a_T + a_H}\), the \(\theta\) becomes the best candidate from the MLE perspective.
  • \[\hat{\theta} = \frac{a_H}{a_H + a_T}\]

Note

압정을 던져 2/5, 3/5 확률이 나오는 것은 아래의 방법을 통해 계산.

binomial distribution, MLE, opmization(derivative).

Number of Trials & Simple Error Bound

  • 시도 횟수가 많아 진다면 무엇이 달라질까?
    • 똑같은 \(\theta\) 값이 나옴.
    • Additional trials reduce the error of our estimation.
    • Right now, we have \(\hat{\theta} = \frac{a_H}{a_H + a_T}, N = a_H + a_T\)
    • Let’s say \(\theta^*\) is the true parameter of the thumbrack flipping for any error, \(\epsilon > 0\)
    • We have a simple upper bound on the probability provided by Hoeffding’s inequality
\[\begin{aligned} P(|\hat{\theta} - \theta ^* \geq \epsilon|) \leq 2 e ^{-2N\epsilon^2} \end{aligned}\]
  • Can you calculate the required number of trials, N?
    • To obtain \(\epsilon\) = 0.1 with 0.01% case

Note

This is Probably Approximate Correct(PAC) learning

Maximum a Posteriori Estimation

Incorporating Prior Knowledge

  • Merge the previous knowledge to my trial
    • \[P(\theta|D) = \frac{P(D|\theta)P(\theta)}{P(D)}\]
      • Posterior = (Likelihood x Prior Knowledge) / Normalizing Constant
    • Already dealt with \(P(D \mid \theta ) = \theta^ {a_H} (1- \theta) ^{a_T}\)
      • \(\theta\)라고 가정하고 이러한 data가 관측될 확률.
    • \(P(\theta)\) is part of the pror knowledge
      • 왜 압정의 앞/뒤가 이런 확률로 나올까?
      • 왜 사람이 이렇게 행동할까?
    • P(D)는 많이 중요하지 않음
      • 사실 \(\theta\)에 대해 관심이 있음.
      • 여러번 시도를 해볼 수 있고, 요즘 data가 많음.
    • \(P( \theta \mid D)\) : Poseterior
      • Then, it is the conclusion influenced by the data and the prior knowledge? Yes, it will be our future prior knowledge!
      • 즉, data가 주어졌을 때 \(\theta\)가 사실일 확률을 표현

More Formula from Bayes Viewpoint

  • \[P(\theta|D) \propto P(D|\theta) P(\theta)\]
    • \[P(D|\theta) = \theta^{a_H} (1-\theta)^{a_T}\]
    • \(P(\theta)\) = ????
      • 어떤 distribution(e.g. binomial distribution)에 의존하여 표현해야함.
      • 50%, 50% 사전 지식을 그대로 사용 불가.
    • 여러 가지 방법이 있으나, 하나의 방법:
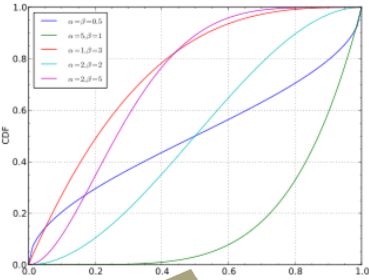
      • Beta distribution, 특정범위내에서 [0,1]로 결합되어 있는 CDF로 표현하여 확률 성격을 잘 표현(아래그림참조)
      • \[P(\theta) = \frac{\theta ^{\alpha-1} (1-\theta)^{\beta -1 }}{B(\alpha, \beta)}, B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}, \Gamma (\alpha) = (\alpha -1 )!\]
An image with a caption
  • Response is
    • \[P(\theta) \propto P(D|\theta) P(\theta) \propto \theta ^{a_H} (1-\theta)^{a_T }\theta ^{\alpha-1} (1-\theta)^{\beta -1 } = \theta ^{a_H + \alpha-1} (1-\theta)^{a_T + \beta -1 }\]

Maximum a Posterior Estimation

  • Goal: the most probable and more approximate \(\theta\)
  • Previously in MLE, we found \(\theta\) from \(\hat{\theta} = argmax_\theta P(D\mid \theta)\)
    • \[P(D| \theta) = \theta ^{a_H} (1-\theta)^{a_T }\]
    • \[\hat{\theta} = argmax_\theta P(D| \theta)\]
  • Now in MAP, we find \(\theta\) from \(\hat{\theta} = argmax_\theta P(\theta \mid D)\)
    • \[P( \theta|D) \propto \theta ^{a_H + \alpha-1} (1-\theta)^{a_T + \beta -1 }\]
    • \[\hat{\theta} = \frac{ \theta ^{a_H + \alpha-1} }{ \theta ^{a_H + \alpha + a_T + \beta -2} }\]
  • The calculation is same because anyhow it is the maximization.

Note

Likelihood에 대해 maximization을 하는 것(MLE)이 아니고, posterior에 관하여 maximization(MAP).

Conclusion from Anecdote

  • If \(a_H\) and \(a_T\) become big, \(\alpha\) and \(\beta\) becomes nothing..
    • But, \(\alpha\) and \(\beta\) are important if I don’t give you more trials.
    • \(\alpha\) and \(\beta\)을 선택함에 따라 결과가 달라짐.
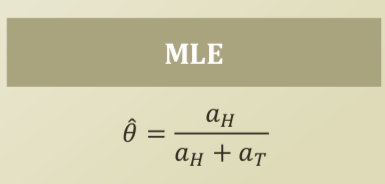
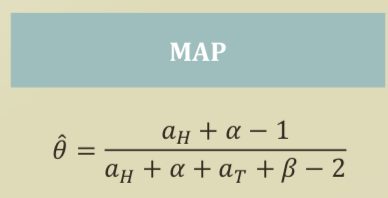
An image with a caption An image with a caption

Basics

Probability

  • Philosophically, Either of the two
    • Objectivists assign numbers to describe states of events, i.e. counting
    • Subjectivists assign numbers by your own belief to events, i.e. betting
  • Mathematically
    • A function with the below characteristics
An image with a caption
\[\begin{aligned} P(E) & \in R \\ P(E) & \leq 0 \\ P(\Omega) & = 1 \\ P(E_1 \cup E_2 \cup \cdots) &= \sum^{\infty}_{i=1} P(E_i) \end{aligned}\]

Conditional Probability

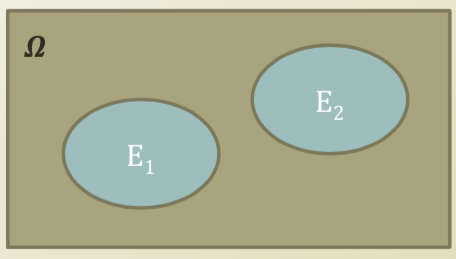
  • We often do not handle the universe, \(\Omega\)
  • Somehow, we always make conditions
    • Assuming that the parameters are X, Y, Z, …
    • Assuming that the events in the scope of X, Y, Z, …
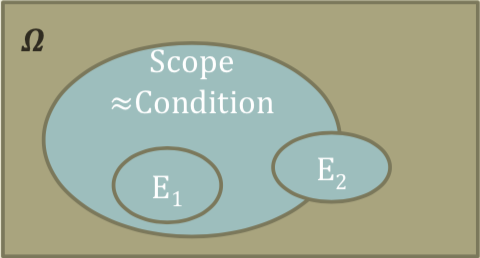
An image with a caption
  • \[P(A \mid B) = \frac{P(A\cap B)}{P(B)}\]
    • The conditional probability of A given B
  • Some handy formular
    • \[P(B \mid A) = \frac{P(A \mid B) P(B)}{P(A)}\]
      • Nice to see that we can switch the condition and the target event
    • Poseterior = (Likelihood X Prior Knowledge) / Normalizing Constant
    • \[P(A) = \sum_{n} P(A \mid B_n) P(B _n)\]
      • Nice to see that we can recover the target event by adding the whole conditional probs and priors

Probability Distribution

  • Probability distribution assigns
    • A probability to a subset of the potential events of a random trial, experiment, survey, etc.
  • A function mapping an event to a probability
    • Because we call it a probability, the probability should keep its own characteristics(or axiomes)
    • An event can be
      • A continuous nemeric value from surveys, trials, experiments …
      • A discrete categorical value from surveys, trials, experiments …
  • For example,
    • f: a probability distribution function
    • x: a continous value
    • f(x): assigned probs \(\begin{aligned} f(x) = \frac{e^{- \frac{1}{2} x^2}}{\sqrt{2 \pi}} \end{aligned}\)
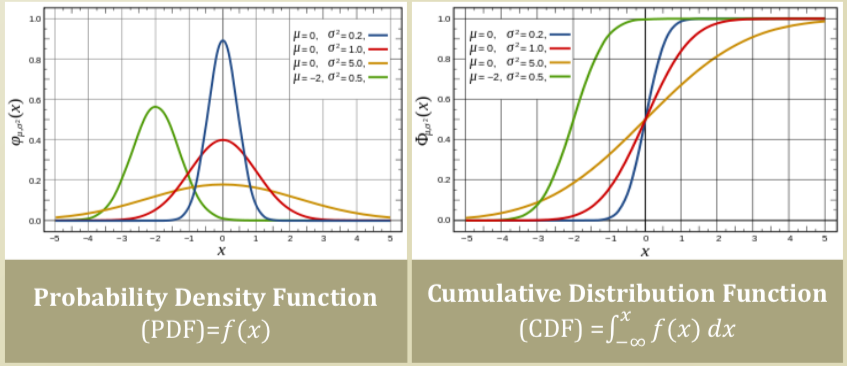
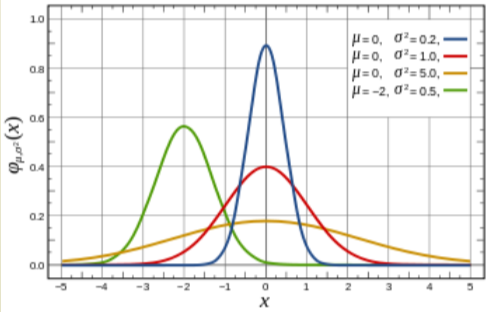
An image with a caption

Normal Distribution

  • Very commonly observed distribution
    • Continuous numerical value
  • \[f(x; \mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} e ^{- \frac{(x - \mu)^2}{2 \sigma ^2}}\]
  • Notation: \(N(\mu, \sigma ^2)\)
  • Mean: \(\mu\)
  • Variance: \(\sigma^2\)
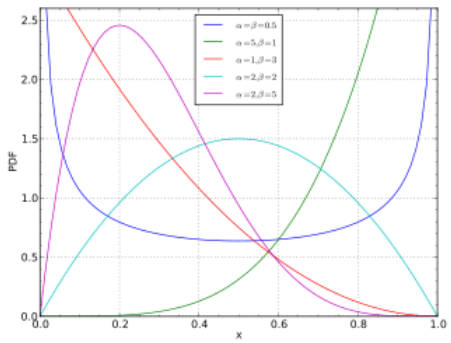
An image with a caption

Beta Distribution

  • Supports a closed interval
    • Continuous numerical value
    • [0,1]
    • Very nice characteristic
    • Why?
      • Matches up the characteristics of probs
  • f(\(\theta\); $$\alpha, \beta\() =\)P \frac{\theta ^{\alpha-1} (1-\theta)^{\beta -1 }}{B(\alpha, \beta)}, B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}, \Gamma (\alpha) = (\alpha -1 )!$$
  • Notation: Beta(\(\alpha, \beta\))
  • Mean: \(\frac{\alpha}{\alpha + \beta}\)
  • Variance: \(\frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta +1)}\)
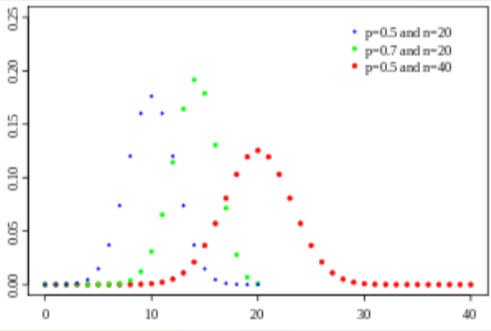
An image with a caption

Binomial Distribution

  • Simplest distribution for discrete values
    • Bernoulli trial, yes or no
    • 0 or 1
    • Selection, switch …
  • \[f(\theta; n, p) = \binom{n}{k} p^k (1-p)^{n-k}, \binom{n}{k} = \frac{n!}{k! (n-k)!}\]
  • Notation: \(B(n,p)\)
  • Mean: \(np\)
  • Variance: \(np(1-p)\)
An image with a caption

Multinomial Distribution

  • The generalization of the binomial distribution
    • e.g., Choose A, B, C, D, E,….,Z
  • \[f(x_1, ..., x_k; n, p_1, ..., p_k) = \frac{n!}{x_1! ... x_k !} p_1^{x_1} \cdot p_k^{x_k}\]
  • Notation: Multi(P), \(P=< p_1, ..., p_k>\)
  • Mean: \(E(x_i) = np_i\)
  • Variance: Var\((x_i) = np_i (1-p_i)\)

Summary

  • 압정 던지는 시도를 통해서 다음번에 무엇이 나올 지 확률을 계산하는 것은 단순히 (횟수/시도) 되는 것이 아니라, 이항분포 가정-> MLE or MAP(사전지식이용) -> optimization(derivative) 과정을 통해 도출되는 것임을 이해했다.

  • MAP는 likelihood를 최대화 하는 MLE 과정에 추가적으로 사전 지식을 사용하기 위해 베이즈 룰을 이용하여 posteriori를 계산하는데 적용이 되었으며, 사전 지식은 Beta 분포(0~1 범위를 가지는 연속분포)라고 가정하여 계산할 수 있었다.

    • 그러나, 결과적으로 시도 횟수가 많아 지게 되면 MLE, MAP는 동일한 결과를 얻을 수 있다.

Reference:

© 2020. All rights reserved.

Powered by Hydejack v8.1.1