[CS294 - 112 정리] Lecture10 - Optimal control and planning
in Reinforcement learning / Reinforcement learning on Cs294
Table of Contents
- Today’s Lecture
- Recap
- Model-based reinforcement learning
- Discrete case: Monte Carlo tree search (MCTS), Stochastic method
- Continous action space
- Stochastic dynamics(Gaussian Dynamics)
- Nonlinear case: DDP/iterative LQR
- Reference
Today’s Lecture
- Model-based reinforcement learning에 대한 소개
- Dynamics를 안다면? 어떻게 decision을 생성할까?
- Monte Carlo tree search(MCTS)
- Trajectory optimization
- Goals:
- Discrete & continous space에서 알고 있는 dynamics를 가지고 planning을 수행하는 방법
Recap
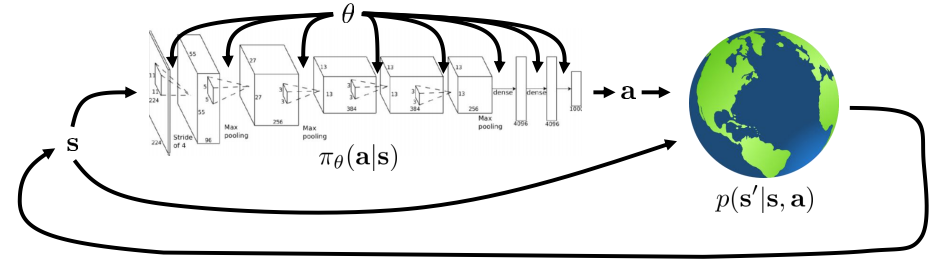
- the reinforcement learning objective
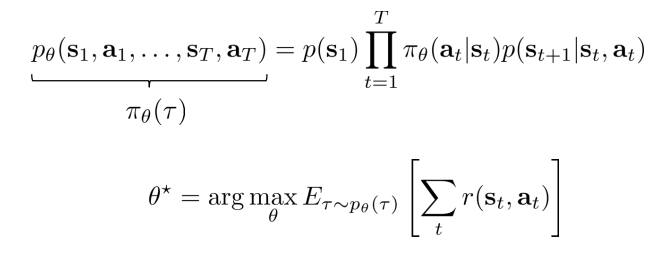
- the model-free reinforcement learning
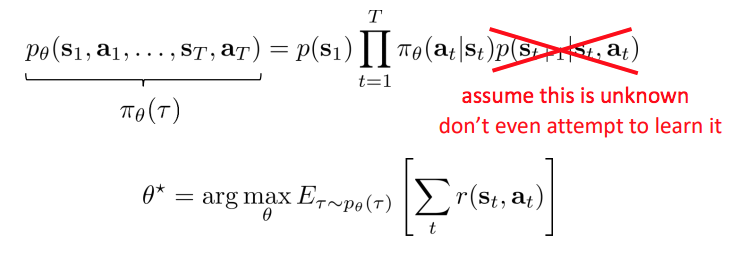
Model-based reinforcement learning
Transition dynamics를 알고 있다면?
- Dynamics를 알고 있는 경우:
- Games(e.g., Go)
- Easily modeled systems (e.g., navigating a car)
- Simulated environments (e.g., simulated robots, video games)
- Dynamics를 학습할 수 있는 경우
- System identification:
- 알고있는 모델의 unknown parameter로 fitting(physical linkage) .
- Learning:
- Observed transition data를 관측하여 general-model(e.g., NN)을 fittng.
- System identification:
- Dynamics를 안다면 더욱 쉽게 만들어 주는가?
- Often, yes!
- 추가적인 learning을 할 필요없이 system을 제어 가능(optimization problem을 푸는 것).
Model-based reinforcement learning
- Mode-based RL: transition dynamics을 학습하고, 어떤 action을 할 것인지 찾기.
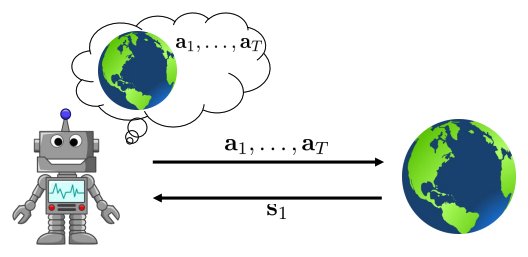
- Today: dynamics를 안다면 어떻게 decision 을 만들 수 있을까?
- System dynamics의 perfect knowledge에서 action을 선택하는 방법.
- Optimal control, trajectory optimization, planning
- Next topic: Unknown dynamics를 학습 하는 방법
- Next topic: Dynamics 학습 후, policy 또한 학습 하는 방법(e.g. by imitating optimal control)
The objective
policy 고려하지 않고 어떤 행동이 좋을 지 생각.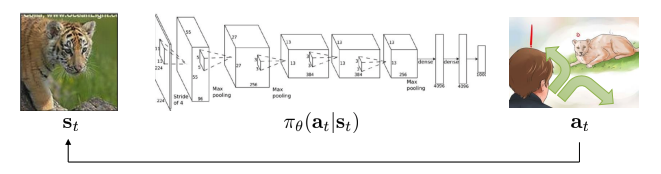
- Cost function:
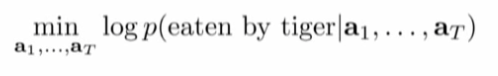
- Constraint optimization problem(deterministic dynamics, 1:T):
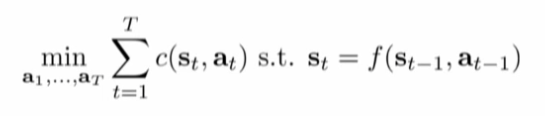
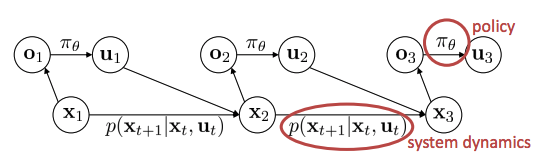
The deterministic case vs stochastic case, open loop case vs closed loop case
- The deterministic case:
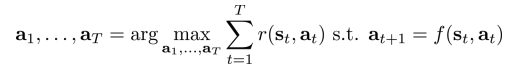
- The stochastic open-loop case:
- Probability distribution이 적용됨.
- Conditional distribution, \(p(s \mid a)\)이 주어지고 expectation이 취해짐.
- why is this suboptimal?
- 기대했던 state로 될 가능성이 적다(HW4).
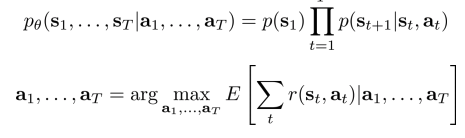
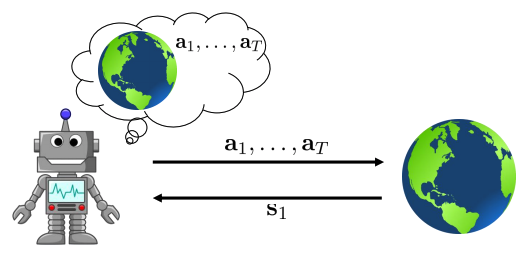
- The closed loop case:
- The open-loop
- 문제점: 원하는 state로 가지못하면, 원하는 성능(목표)을 얻지 못한다.
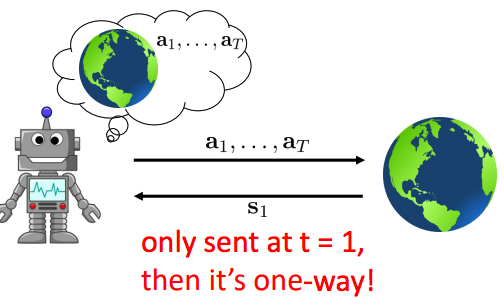
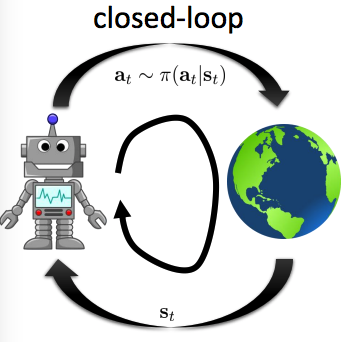
따라서, deterministic이 아닌 경우(=stochastic)에는 closed loop를 사용해야만 한다.
The stochastic closed-loop case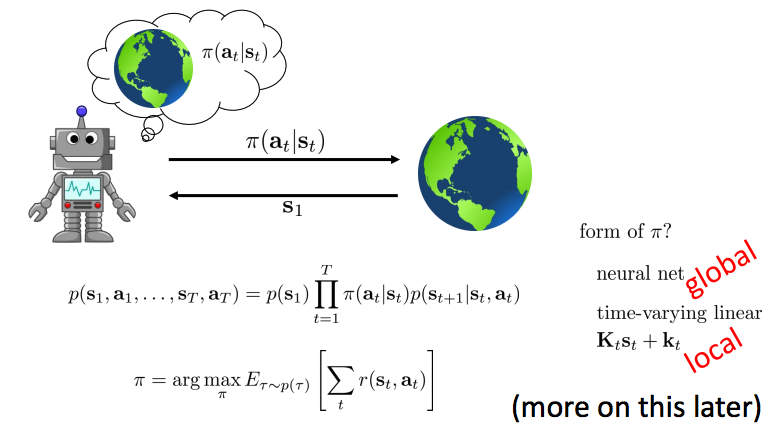
Stochastic optimization
- Optimal control/ planning:
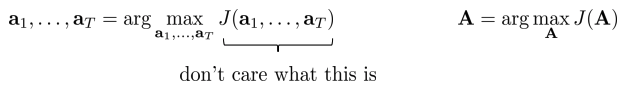
- \(1.\) Simplest method: guess & check, “random shooting method”
- Some distribution(e.g., uniform)에서 \(A_1,..., A_N\) 선택
- Argmax\(_i J(A_i)\) 기반하여 \(A_i\) 선택
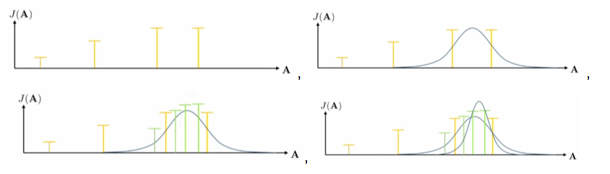
- \(2.\) Cross-entropy method(CEM)
- Some distribution이 아닌 더 좋은 방법은 무엇일까?
- Continuous-valued input을 가진 cross-entropy method:
- p(A)에서 \(A_1, ..., A_N\) 샘플링
- \(J(A_1), ..., J(A_N)\) 평가
- 값이 큰 elites \(A_{i_1}, ..., A_{i_M}\) 선택, where M < N
- p(A)를 \(A_{i_1}, ..., A_{i_M}\)로 refit.
- 일반적으로 Gaussian distribution 사용.
- see also: CMA-ES(momentum을 가지고 CEM을 사용하는 방법 또한 존재)
- 장점:
- Parallelized하면 매우 빠름.
- 매우 단순.
- 문제점:
- 매우 까다로운 dimensionality limit.
- 오직 open-loop planning 에서 사용가능.
Discrete case: Monte Carlo tree search (MCTS), Stochastic method
- Search 문제와 같은 discrete planning
- 모든 state, action에 대하여 값을 가지고 있는 것은 힘듬.
- Full tree없이 값을 근사하는 방법
- Policy를 이용하여 tree를 expansion.
- 모든 경로를 search할 수는 없다 - 어디를 첫 번째로 search?
- 다음 state에서의 score가 큰 것(방문 횟수와 받을 score의 합으로 계산됨)을 선택
Intuition: best reward의 node 선택하지만, 방문했던 node는 덜 선호.
- Generic MCTS
- Tree Policy(\(s_{1l}\)) 사용하여 leaf \(s_l\) 찾기
- DefaultPolicy(\(s_l\)) 사용하여 leaf 평가
- \(s_1\) 및 \(s_l\) 간의 tree의 모든 값들 update.
- \(s_1\) 에서 best action 선택(1~3 반복)
- UCT Tree Policy(\(s_t\))
- \(s_t\) 가 not fully expanded, 새로운 \(a_t\) 를 선택하고
- 아니라면(fully expanded), best Score(st+1)으로 child 선택
- C는 hyper parameter.
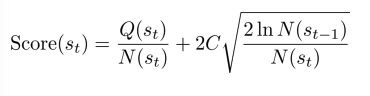
Continous action space
Can we use derivatives?
- Action sequence를 derivative하여 optimization.
- Cost function을 사용한 constrained 문제, unconstrained 문제(elimination method 사용)가 있다
- 일반적으로 back propagation을 통해 미분하고 최적화 진행.
- 실전에서는, 1차 미분방법(first order gradient descent)을 사용하면 매우 민감하기 때문에, chain rule을 적용하면 매우 작은 값이거나 매우 큰 값이 되기 때문에 2차 미분 을 사용

Shooting methods vs Collocation method
Shooting method: optimize over actions only, unconstrained optimization problem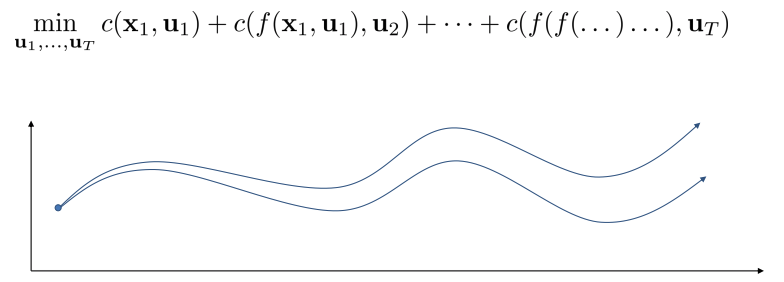
Collocation method: optimize over actions and states, with constraints, constrained optimization problem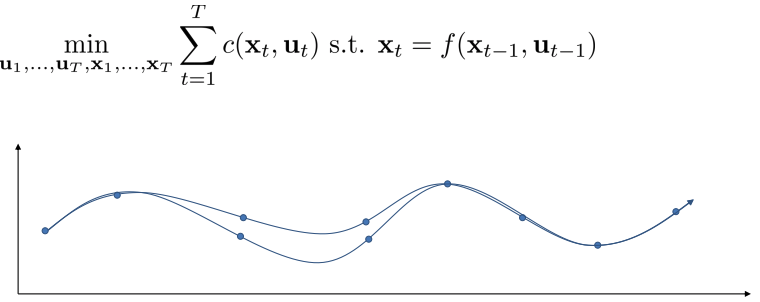
자세한 내용: Trajectory optimization
Linear case: LQR
- Dynamics: linear
- Cost funtion: quadratic
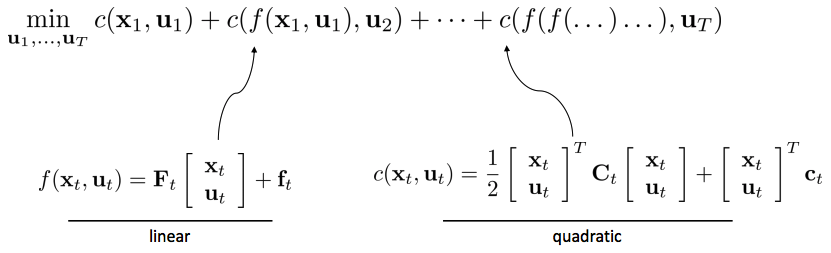
Note:
- \(Q_T, q_T, Q(,)\): terminal value를 포함한 cost function의 합
- \(V_T, v_T, V(,)\): state feedback control로 대체하여 Q fucntion 표현.
입력은 state feedback controller.
- T인 경우.

- T-1인 경우.

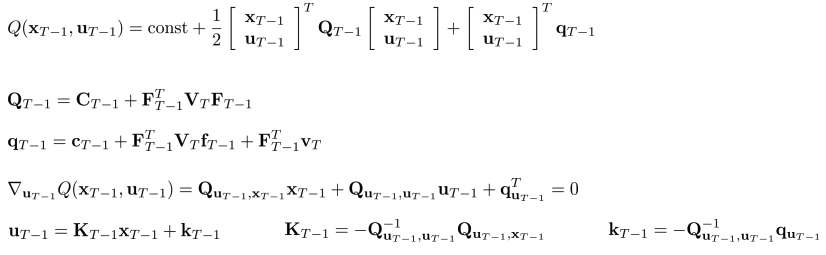
- T부터 1까지의 process:
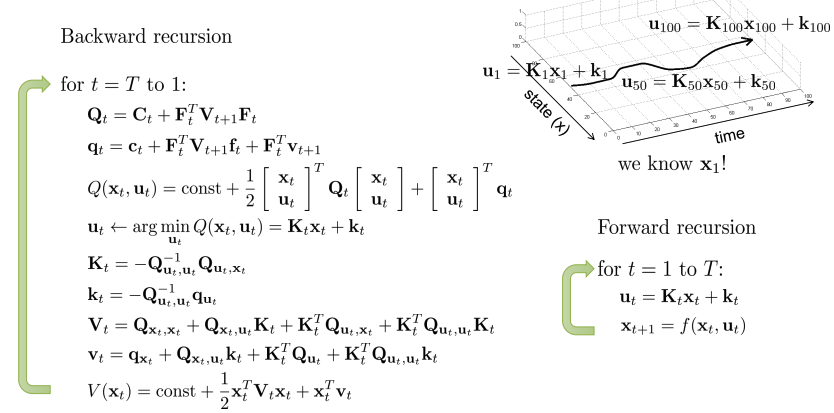
Some useful definitions:
- T 에서부터 backward 방향으로 매 스텝마다 Q, q계산, u 찾기, K,k, 계산, V,v 계산
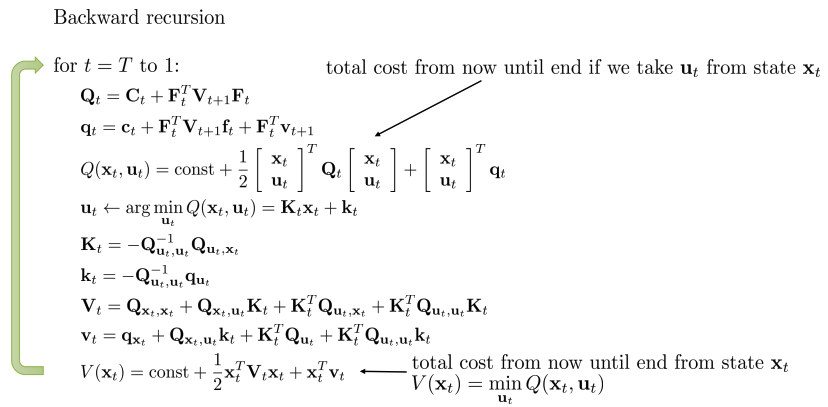
Stochastic dynamics(Gaussian Dynamics)
- Distribution에서 picking.
- Zero mean noise를 추가.
- Dynamics가 확률에 기반하여 sampling.
- Gaussian distribution 모델을 주로 사용.

Nonlinear case: DDP/iterative LQR
- Linear-quadratic assumptions:
- Dynamics: linear
- Cost function: quadratic
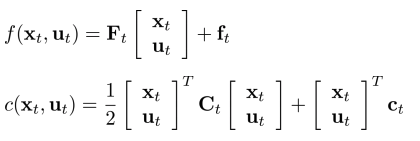
- Nonlinear system을 linear quadratic system으로 approximation 할 수 있을까?
- Dynamics는 Tayler 1차 근사, cost function은 Tayler 2차 근사
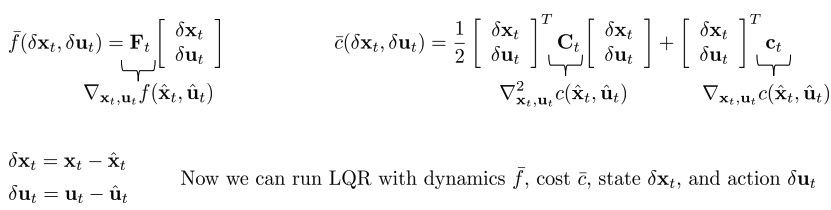
Iterative LQR

- 어떻게 동작?
- min \(_x\) g(x) 계산을 위한 Newton’s mothod와 상당히 유사.
- Iterative LQR(iLQR) idea: Taylor expansion 을 통해 complex nonlinear function을 locally approximation.
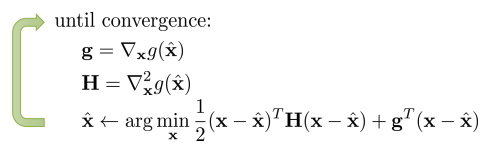
- iLQR은 다음을 풀기위한 Newton’s method의 approximation(2차 근사)
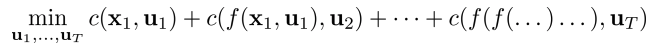
Differential dynamics programming(DDP)
- Newton’s method는 2차 dynamics 근사를 필요로 한다(연산량 상당)
- 2차 근사를 제거하여 사용: DDP
- 지금까지의 단점: 모델 2차 근사(Newton’s method)
- 모델은 2차가 아니므로 수렴이 잘 안될 수도 있다 -> back tracking idea를 이용하여 사용(알파, step size도입)
