[CS294 - 112 정리] Lecture11 - Model-Based Reinforcement Learning

in Reinforcement learning / Reinforcement learning on Cs294

Table of Contents

  1. Overview
  2. Today’s Lecture
  3. Model-based reinforcement learning
  4. Summary
    1. The trouble with global models
  5. Local models
    1. What controller to execute?
    2. How to fit the dynamics(Dynamics를 어떻게 fitting)?
  6. Real problem
  7. Digression: dual gradient descent
    1. Dual gradient descent
    2. Dual gradient descent with iterative LQR__
  8. Trust regions & trajectory distributions
  9. Reference

Overview

  1. 지난 강의:
    • 알고있는 system dynamics(e.g., physics)를 통해 backpropagating(or planning)하여 자체적으로 좋은 action을 선택.
  2. 이번 강의: dynamics 를 모른다면 어떻게 해야할까?
    1. Fitting global dynamics models (“model-based RL”).
    2. Fitting local dynamics models.
  3. 다음 강의:
    • Image들과 같이 높은 차원 observation에 대해 dynamics를 학습.
  4. 다다음 강의:
    • Optimal control의 목표를 가지고 NN policies를 학습하기 위해 optimal control과 policy search 결합.

Today’s Lecture

  1. Overview of model-based RL
    1. Model만 학습
    2. Model & policy 학습
  2. 어떤 모델을 사용할 수 있을까?
  3. Global model & local model
  4. Local model 및 trust region 학습
  • Goals:
    • Model-based RL의 용어 및 구조 이해
    • Model-based RL에서 사용할 수 있는 모델 종류 이해
    • Model learning의 실제 고려사항 이해
  • But, Deep RL은 이후에 다룰 예정.

Model-based reinforcement learning

Why learn the model?

  • 아래의 빨간원으로 표현되는 미분 값을 알면 model을 이용할 수 있다.
  • 즉, Deterministic case에서 \(f(s_t, a_t) = s_{t+1}\)을 안다면, 이전에 배웠던 optimal control와 같은 방법(planning) 들을 사용할 수 있다
    • 다른 경우: stochastic case, \(p(s_{t+1} \mid s_t, a_t)\).
  • Data로부터 \(f(s_t,a_t)\)을 학습하고, 이를 통해 planning
An image with a caption
  • Model-based reinforcement learning version 0.5:
    1. Base policy \(π_0 (s_t, a_t)\) (e.g., random policy)을 구동하여 \(D = {(s, a, s’)_i}\) 수집.
    2. \(\sum_i \left \| f(s_i, a_i) - s' _i \right \|\)를 최소화하여 dynamics model f(s, a) 학습.
      1. Deterministic case: 위와 같이 regression loss(MSE).
      2. Stochstic인 case: maximizing the likelihood(log \(p(s' \bar a,s)\)).
      3. Gaussian distribution인 경우에는 동일함.
    3. Action을 선택하기 위해 f(s, a) 를 통해 planning.
An image with a caption

1, 2 과정은 supervised learning과 유사하며, 3 과정은 지난번에 했던 내용(LQR, iLQR, DDP 사용).

  • MBRL 0.5은 잘 동작?
    • 그래도 많은 영역에서 동작!
    • 본질적으로 system identification(입력과 출력을 모델링하는 것, physical parameters를 찾는것)이 classical robotics에서 동작하는 방식 이므로 동작.
    • 좋은 base policy를 설계하기 위해서 어느정도 주의를 기울여야한다.
      • 만약 물리학의 지식을 사용하여 dynamics representation을 수작업으로 처리하고 몇 가지 parameter를 fitting하면 특히 효과적.
  • 그러나, 일반적으로는 동작하지 않음.
    • Imitation learning에 대해 언급했던 것과 동일한 이유(Distribution mismatch 문제)
      • 예제 목표: 산의 정상으로 가는것.
        1. Base policy(π0) = random (빨간 선, 비탈길에서 걸음)
        2. Dynamics model 학습
          • 오른쪽으로 갈때 정상으로 올라감
        3. 항상 true는 아님.
          • 주어진 데이터를 기반으로 학습이 진행되기 때문.
      • Why this problem(왜 추락할까)?
        • Base policy는 some distribution \(P_{π_0}(s_t)\)로부터 data를 제공
          • 최종 \(p_{π_f}(s_t)\)와 base \(p_{π_0}(s_t)\)의 distribution이 동일하지 않음.
          • \(p_{π_0}(s_t)\)를 아무리 잘 generlization해도 보장할 수 없다.
  • 새로운 training data를 활용 해 supervised learning을 통해 low generalization error을 가질 수 있다.
    • Arbitrary distribution으로 하게되면 보장할 수 없음.
    • 이러한 것이 DAGGER와 유사.
An image with a caption

Distribution mismatch 문제는 모델 class가 더욱 expressive할수록 더욱 악화(exacerbated).

Can we do better?

  • 성능 향상을 위해, 이전의 문제였던 distribution mismatch를 해결
    • \(p_{\pi_F}(s_t)\)에서 data를 수집하여 \(p_{\pi_o}(s_t) = p_{\pi_f}(s_t)\) 조건 추가
  • Model-based reinforcement learning version 1.0:
    1. Base policy \(π_0 (s_t, a_t)\)(e.g., random policy)을 구동하여 D = { \((s, a, s’)_i\) } 수집.
    2. \(\sum_i \left \| f(s_i, a_i) - s' _i \right \|\)를 최소화하기 위해 dynamics model f(s, a) 학습.
    3. Action을 선택하기 위해 f(s, a)를 통해 planning.
    4. 위의 action을 실행하고 결과 data {\((s, a, s’)_j\)} 를 D에 추가
An image with a caption
  • 문제점: 만약 실수를 하게 된다면(우리가 원한 state로 도달하지 않을 경우)?
    • Small error라도 축적되면 재앙이됨.
      • 전진으로 가는 것인데 조금씩 왼쪽으로 가게되면 많이 벗어나게됨
    • 해결책: Model error를 replanning.
An image with a caption
  • Model-based reinforcement learning version 1.5: 1. Base policy \(π_0 (s_t, a_t)\)(e.g., random policy)을 구동하여 D = { \((s, a, s’)_i\) } 수집. 2. \(\sum_i \left \| f(s_i, a_i) - s' _i \right \|\)를 최소화하기 위해 dynamics model f(s, a) 학습. 3. Action을 선택하기 위해 f(s, a)를 통해 planning 4. 첫번째 계획된 action을 실행하고, 결과 state s’를 관측(MPC) * Generate a new plan which will hopefully correct that mistake
    * MPC가 유용한 이유는 모델이 완벽하지 않아도 replanning하여 policy의 실수에 대해 수정해준다. 5. (s, a, s’)를 dataset D에 append
An image with a caption
  • Replan하는 방법(How to replan?).
    • Replan을 할수록, 각 개별 완벽한 plan은 덜 필요하게 됨.
    • 짧은 horizon 사용 가능
    • 심지어 random sampling도 종종 잘동작.
      • huge long plan을 생성할수록 잘 동작
An image with a caption
  • 단점: That seems like a lot of work…, 많은 연산 필요 - 3 step(replanning)
    • But, 다음주에 우측하단 방법을 사용하여 policy를 distill(증류)시킴(demonstration에서 supervising)
    • 이를 학습시키고 test할 때는 cheaper policy 사용
An image with a caption
  • 지금까지는 모델을 학습하고 optimal control 기법을 이용하여 action 선택(computational power가 expensive)
  • Model-based reinforcement learning version 2.0:
    • Policy를 backpropagate해서 직접 학습 할 수 있을까?
    • f(s,a)를 backpropagate해서 policy optimization (3번 과정, second optimization)
    • 아래의 그림에서는 deterministic이라고 가정,
      • Stochastic경우, reparameterization trick 을 이용하여 generalization.
    • 그러나, NN은 종종 잘 동작하지 않음.
      • Vanishing gradient 문제.
      • recurrent NN을 사용하여 해결 가능.
An image with a caption

Summary

An image with a caption

Case study: model-based policy search with GPs(version 2.0, 2011)

An image with a caption
  1. Base policy \(π_0 (s_t, a_t)\) (e.g., random policy)을 구동하여 D = { \((s, a, s’)_i\) } 수집.
  2. GP를 사용하여 Bayesian nonparametric model 을 사용
    • Good uncertainty estimate
  3. \(\pi_\theta(a_t \mid s_t)\)을 최적화하기 위해서 \(p(s’ \mid s, a)\) 을 통해 policy로 back propagate
    • Contribution: backpropagation은 fairly tractable 및 stable하게 만듬.

Step 3에 대해 자세히 알아보자

  • Stochastic model
    • \(p(s_t)\) 가 주어지면, \(p(s_{t+1})\)을 계산하기 위해 \(p(s’ \bar s, a)\) 사용 (state marginals 계산하기 위해 approximation을 formulate)
      • 만약 current state marginal \(p(s_t)\) 가 Gaussian이면, closed form으로 (non-Gaussian distribution) 을 얻을 수 있다.
      • Moment matching 을 사용해서 non-Gaussian 을 Gaussian \(p(s_{t+1})\) 으로 projection.
      • The other property:
        • 만약 reward가 nice하고 p(s)가 Gaussian이라면, \(E_{s \sim p(s)}\)r(s)은 easy.
        • 많은 함수가 있으며, Gaussian하에서 expression에 대한 analytic closed-form expression을 가진다(quadratic function)
    • \(\sum_t E_{s \sim p(s_t)}[r(s_t)]\)을 쓰고 미분*
      • Expected reward의 합을 미분.
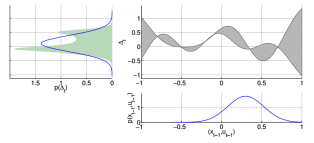
An image with a caption
  • Green: prediction, 그에 따라 gaussian approximation

사용가능한 모델 종류(What kind of models can we use)?

  • GP를 model based rl에서 많이 사용
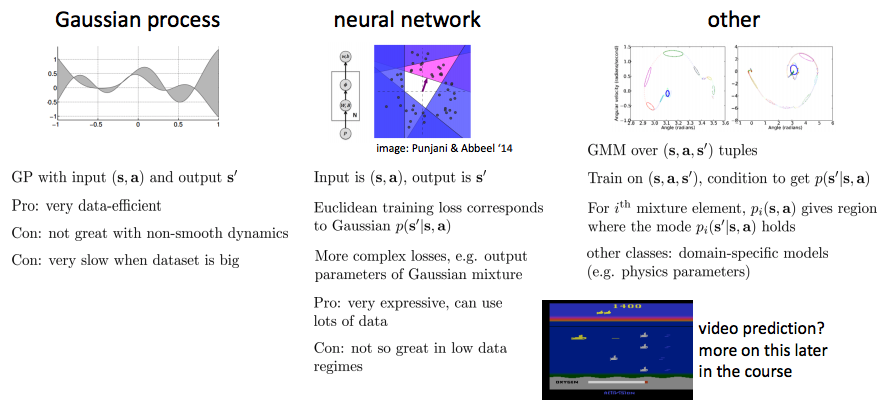
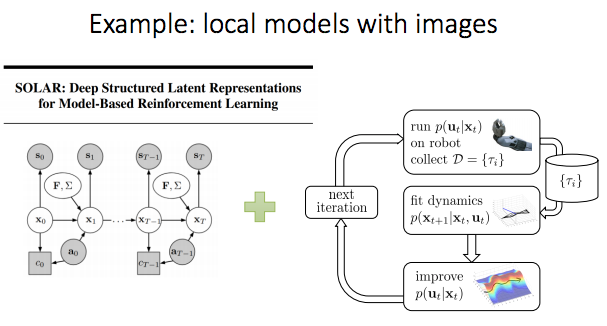
An image with a caption

  • 지금까지는 low dimension에 관련해서 진행, image와 같은 high capacity model의 경우는 다음 번에 다룰 것.

  • Question: policy와 model의 approximation을 공유하는 것은 어떨까?

    • 전혀 다른 것이므로 기본적으로 시도하기에 적합하지 않음.

HW4와 밀접한 연관이 있는 것:

  • Dynamics model은 NN으로 표현.
  • Mujoco 벤치마크.
An image with a caption

The trouble with global models

  • Global model: Big neural network에 의해 나타나는 \(f(s_t, a_t)\)
    • 우리의 목표는 모든 world의 dynamics를 정확하게 모델링 하는 것.
An image with a caption
  • Model이 erroneously optimistic인 곳을 planner(or policy)가 찾아 낼 것.
    • Planner는 모델에 따라 최적화됨.
    • 비록 정확하지 않은 (or 실수로든) 모델이 High reward를 받기 위해 생각하는 부정확한 어떠한 곳라도 planner는 행동하게 됨.
  • 좋은 solution에 수렴하기 위해서 대부분 state space에서 매우 좋은 model을 찾아야한다.
    • 이번 강의에서는 하나의 solution만 다룸.
  • 일부 작업에서, global model은 학습하고자 하는 behavioral skill(policy)보다 더욱 복잡하다.
    • 물리적 현상은 cup에서 손가락의 contact, 물의 출렁거림은 복잡.
    • But, 행동(policy)은 그냥 물컵을 holding하면 됨.

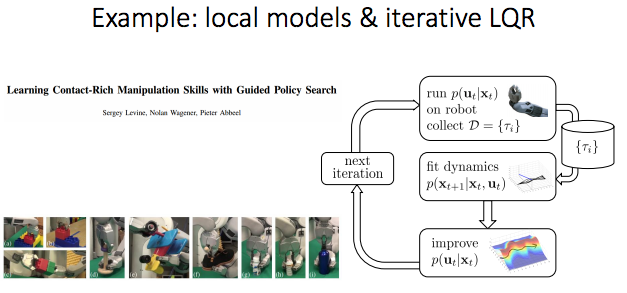
Local models

  • 처음은 dynamics(f)를 모르는 상태이므로 학습을 필요 로 한다.
  • 그러기 위해서는 \(\frac{df}{dx_t}, \frac{df}{du_t}\)을 알아야 한다(Talyor expansion을 이용하여 근사).
    • 매 time step, policy(or trajectory)에 따라 linear regression 방법 등으로 fitting.
    • 아래의 그림은 5개의 경로가 존재하며, state space의 진행과정들(trajectories)을 보여줌
    • 이 경로를 매 tim estep마다 linear approximation
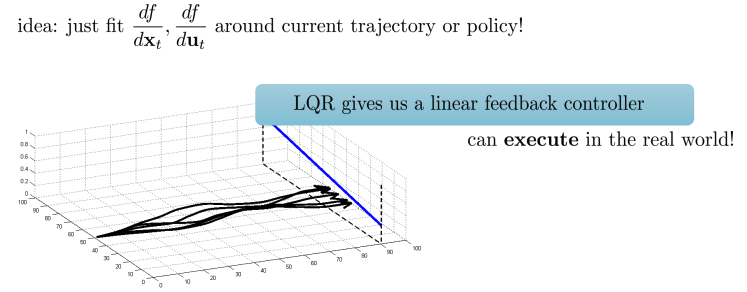
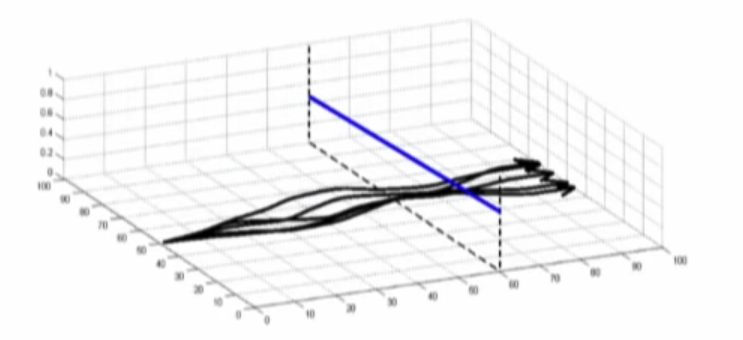
An image with a caption
An image with a caption
An image with a caption
  • Some trajectories를 수집하여 linearized dynamics(\(\frac{df}{dx_t}, \frac{df}{du_t}\))을 fitting.
    • Dynamics는 Gaussian noise 고려
    • Dynamics는 linearization을 통해 approximation
      • A, B는 미분하여 구하게 됨.
      • Local이라고 말하는 이유는 LQR을 사용하기위해서 dynamics를 어떤 지점에서 선형근사 하기 때문이다. 이것은 global하게 동작하지 않는다.
  • 아래의 구조는 basic idea
    • 몇 개의 issue가 존재.
      • 어떤 controller를 사용하여 right(옳은) data를 얻을 지.
        • 아래에서 다룸.
      • Global하게 다뤄지지 않고 있기 때문에, local을 벗어나면 발산하는 문제를 해결해야함.
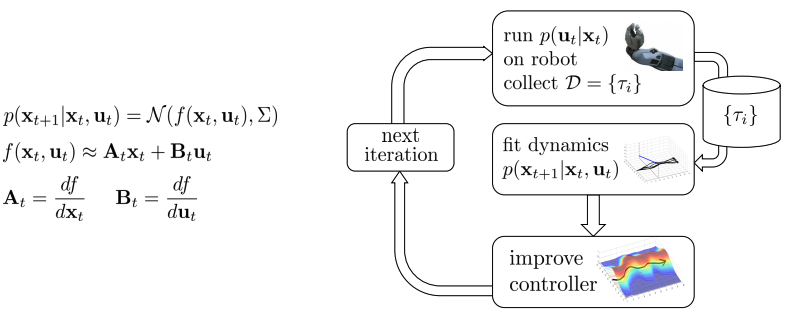
An image with a caption

What controller to execute?

  • Iterative LQR
    • Linear feedback control(closed loop, shooting method)
    • Nonlinear를 linear로 근사 시켜 제어(이 과정에서 deviation이 발생)
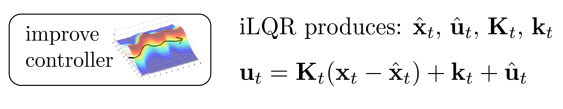
An image with a caption
  • Version 0.5(deterministic controller)
    • Deviation이나 drift가 일치하지 않음(근사후 \(u_t\)로 바로사용함, 조정하지 않음)
    • 문제점: not exploration, numerical issue
  • Version 1.0
    • 성능 조금 향상(근사 후 \(u_t\)로 바로 사용하지 않고 조정했지만, 완벽하게 재구현하지는 못함)
    • 문제점: Linear regression을 진행하게 되면, 샘플에 따라 linear fit이 달라짐. 한 군데에 몰려있으면, 근사가 정확하지 않음 -> 노이즈를 추가하여 spread 필요
      • (deterministic경우 linear regression이 잘 동작하지 않음)
  • Version 2.0
    • 모든 sample이 같지 않도록 noise 추가
      • 어떻게 노이즈 추가? Heuristic
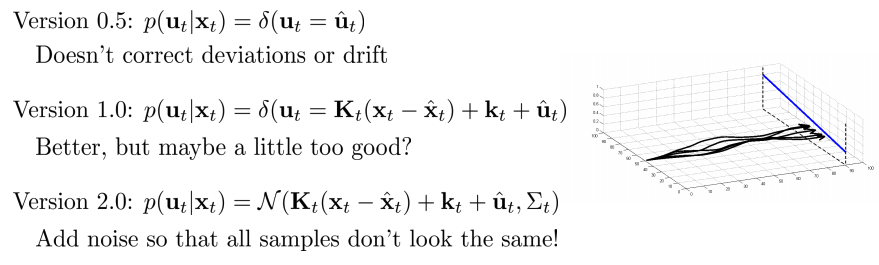
An image with a caption
  • 노이즈를 추가하는 법.
    • \(\sum_t Q^{-1}_{u_t, u_t}\)(Intuitive interpretation이면서 theoretical interpretation도 가진다)
    • \(Q(x_t, u_t)\)는 cost to go: action을 취한 후에 얻게 되는 total cost.
      • Action이 문제가 되지 않은 경우에 더 많은 noise를 주입하여 Q matrix 구성
      • \(u_t\)를 변경하여 Q-value은 많이 변하면 \(Q_{u,u}\)는 크다(Q function의 curvature는 매우 sharp하기 때문)
      • Cost to go에 최소한의 영향을 줄때만 random하게 행동
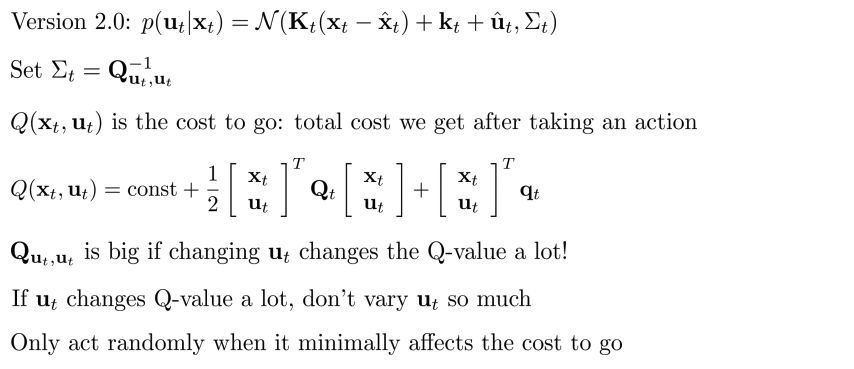
An image with a caption
  • Standard LQR:
    • Total cost를 최소화, \(\sum^T_{t=1} c(x_t,u_t)\)
  • Linear Gaussian:
    • min \(\sum^T_{t=1} E_{(x_t, u_t) \sim p(x_t, u_t)} [c(x_t,u_t) - H(p(u_t \mid x_t))]\)
    • Maximum entropy solution: cost를 최소화하며 가능한한 random 하게 행동하는 것.
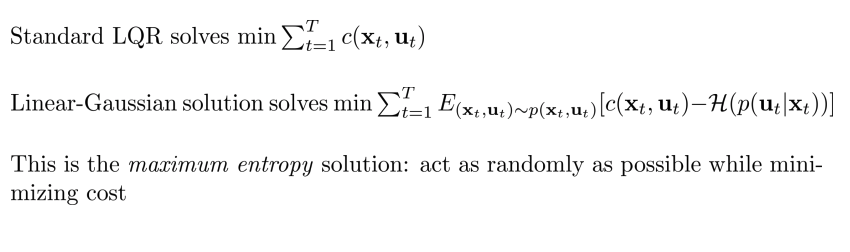
An image with a caption

Local models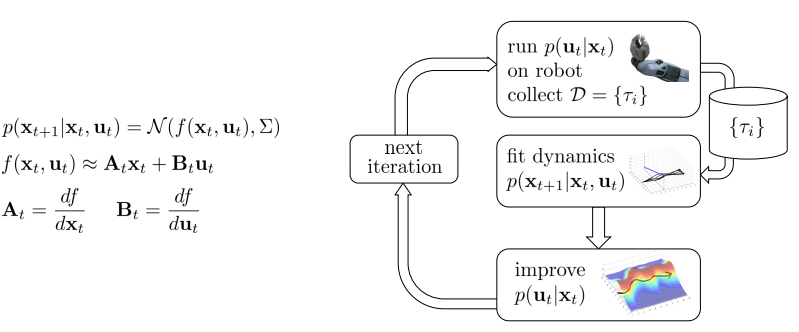

An image with a caption

How to fit the dynamics(Dynamics를 어떻게 fitting)?

An image with a caption
  • Version 1.0: linear regression을 사용 하여 각 time step에서 \(p(x_{t+1} \mid x_t, u_t)\) fitting.
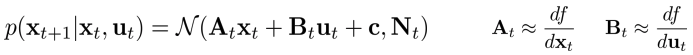
An image with a caption
  • Version 2.0: Bayesian linear regression 사용 하여 p\(p(x_{t+1} \mid x_t, u_t)\) fitting
    • 매우 좋은 아이디어는 아니지만, sample이 충분하다면 동작.
    • Prior(GP, deep net, GMM)으로 선호하는 global model을 사용(사전지식사용, 실제로 이용은 아님)

Real problem

What if we go too far?

  • Linearize된 local model은 small region에서만 정확.
  • Policy를 유지하는 constraint를 부과해야한다.
  • 초록색: real dynamics(nonlinear), 파란색: linearized estimate of dynaimcs, 빨간색: big error
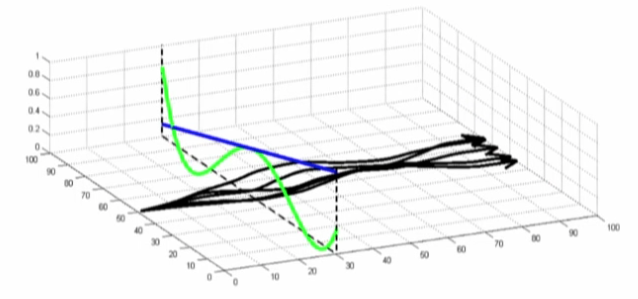
An image with a caption
  • LQR을 사용했을때 파란 dotted line은 원하는 결과지만, local model이므로 빨간 dotted line이 실제 결과
    • 따라서, LQR의 solution에 대한 추가 constraint에 대한 이해가 필요하며 검은 line에 가깝게 유지해야한다.
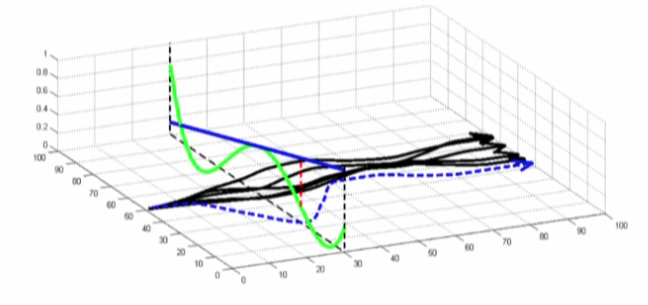
An image with a caption

How to stay close to old controller?

  • IDEA: Natural gradient와 KL divergence constraint 매우 유사
    • KL divergence와 trajectory state, action 간의 관계의 분석
  • Controller \(p(u_t, x_t)\) : linear Gaussian,

  • Trajectory distribution p(τ): big product of policy and dynamics

  • 직관:
    • old \(\bar{p}(\tau)\)와 가까운 new \({p(\tau)\)라면?
      • 만약 trajectory distribution이 가깝다면, dynamics도 가까울 것
      • 가깝다라는 것은 무엇을 의미하는가? \(D_{KL} (p(\tau) \mid \mid \bar{p}(\tau)) \geq \epsilon\)
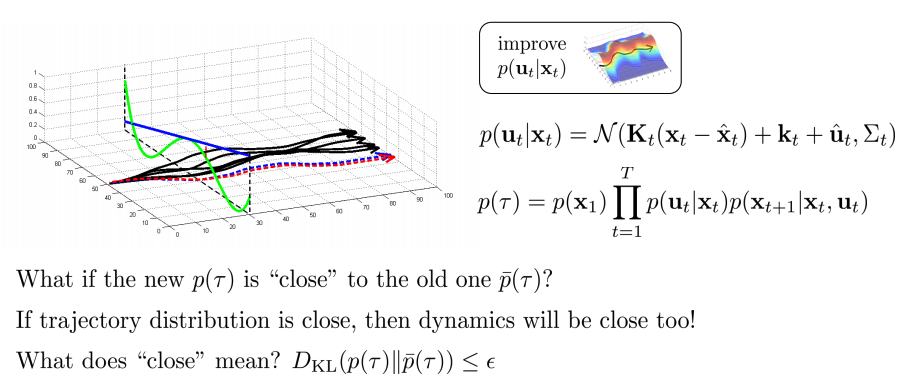
An image with a caption

KL-divergences between trajectories

  • PG에서 trust region과 상당히 유사
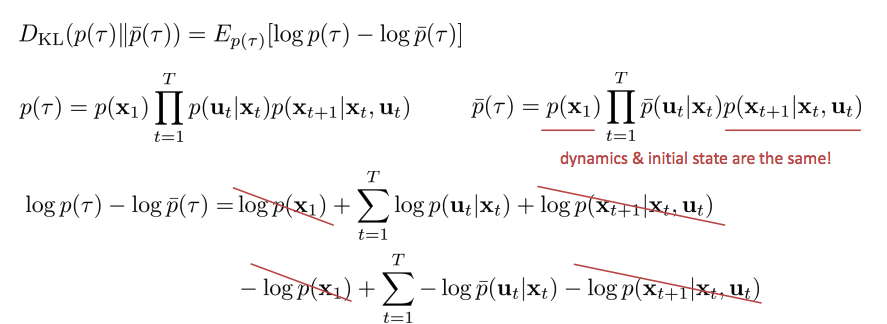
An image with a caption
  • log\(p(u_t \mid x_t)\)는 새로운 controller를 optimization하는 것.
    • State marginal의 expectation으로 동등하게 풀어 쓸 수 있으며 negative entropy이므로 \(-H\)로 대체 가능.
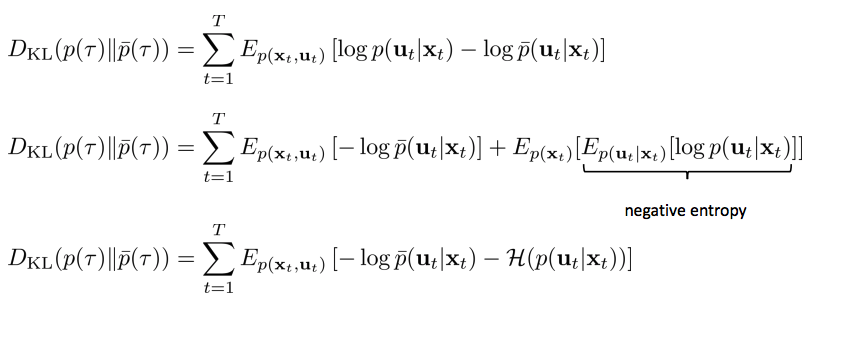
An image with a caption

  • Reminder: Linear-Gaussian 은 \(\sum^T_{t=1} E_{p(x_t,u_t)} [c(x_t, u_t) -H(p(u_t \mid x_t))]\) 를 최소화하는 문제를 풀 수 있다.

  • \(D_{KL}\)을 cost에 넣을 수 있다면, iLQR을 동작 가능.

    • But How? constraint로 추가.
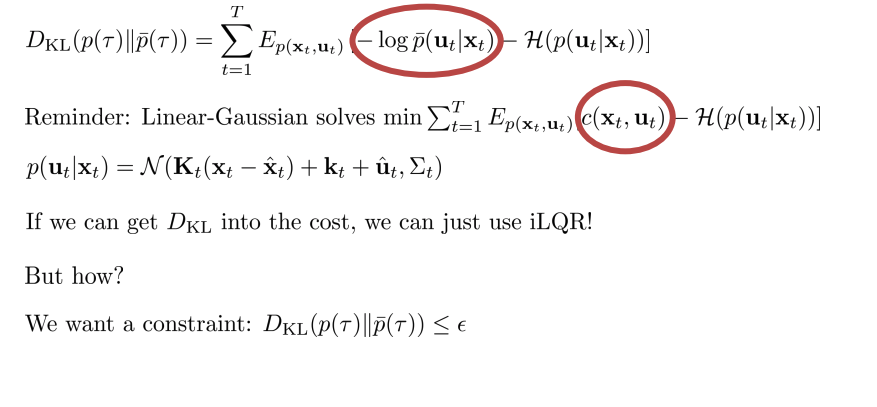
An image with a caption

Digression: dual gradient descent

Dual gradient descent

  • Constrainted optimization 문제 푸는 법: Lagrangian multiplier 이용하여 dual 문제로 변경하여 solution 찾음
    • \(g(\lambda)\): dual function.
    • \(\lambda\)를 maximization: constraint optimization문제를 푸는 것.
      • Compute the gradient!
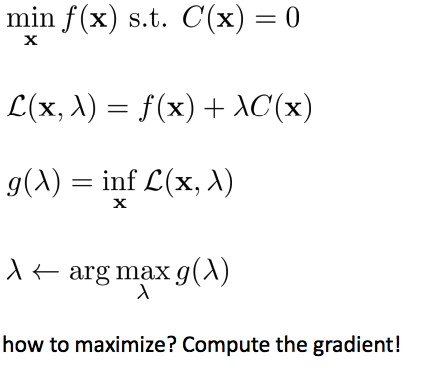
An image with a caption
  • \(x^* = argmin_x L(x, \lambda)\)에 의해 주어진 dual variable에 대한 Lagrangian을 최소화.
  • Gradient step으로 complicated constrainted optimization문제 품.
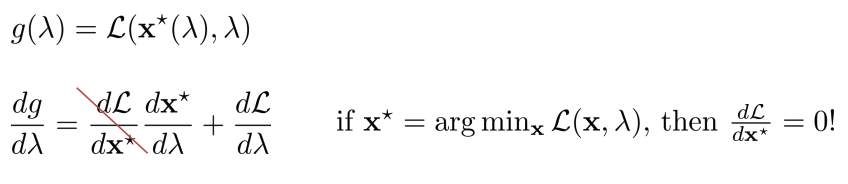
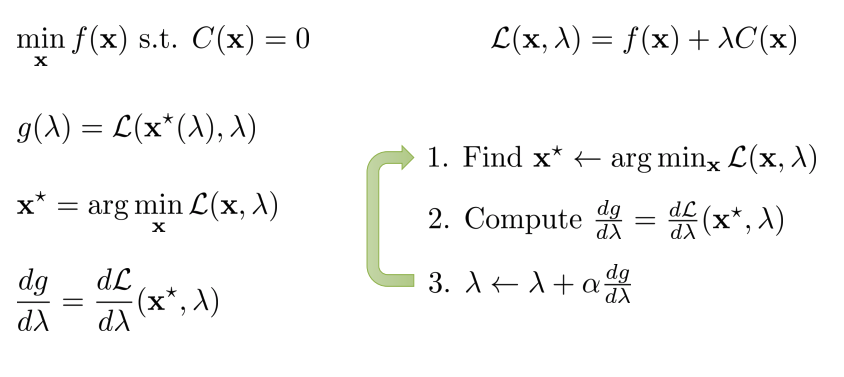
An image with a caption
An image with a caption

Dual gradient descent with iterative LQR__

  • KL divergency constraint를 추가하여 dual gradient descent로 solution을 찾는 과정
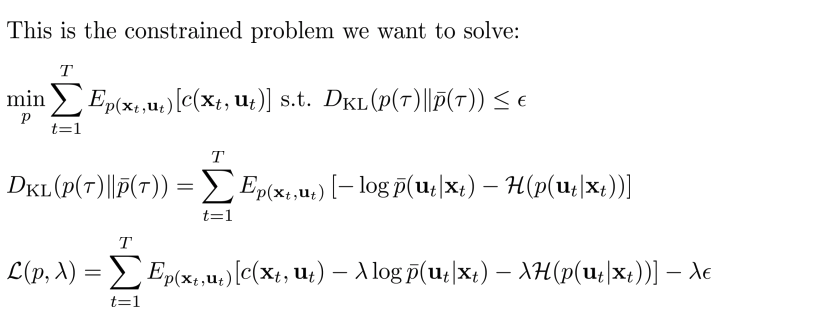
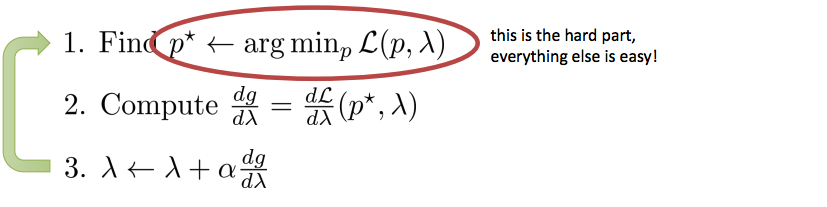
An image with a caption
An image with a caption
  • 1번 부분이 어려운 부분(hard part,everything else is easy)
    • Idea: cost를 최소화하는 과정이 이미 LQR에서 이러한 과정을 진행
    • cost를 약간 변경하여 사용.
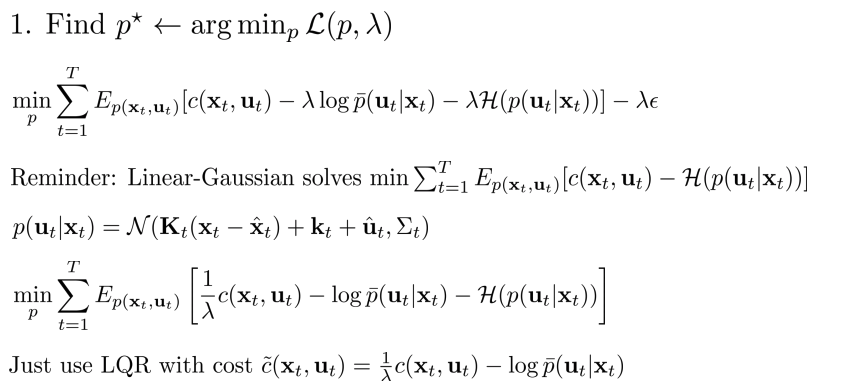
An image with a caption
An image with a caption

Trust regions & trajectory distributions

  • Linear-Gaussian 혹은 더욱 복잡한 것(e.g., NN)이든 , 두 policy 혹은 controller간의 KL-divergences를 bounding하는 것은 실제로 유용.
  • Policy들을 KL-divergence를 bounding은 trajectory distribution들간의 KL-divergence를 bounding한 것과 동일.
An image with a caption
An image with a caption
An image with a caption

Reference

CS294-112 Lecture11

© 2020. All rights reserved.

Powered by Hydejack v8.1.1