[CS294 - 112 정리] Lecture13 - Learning Policies by Imitating Other Policies
in Reinforcement learning / Reinforcement learning on Cs294
Table of Contents
- Overview
- Today’s Lecture
- So how can we train policies?
- General guided policy search scheme
- Model-based RL algorithms summary__
- Limitations of model-based RL
- which algorithm do I use?
- Reference
Overview
- 지난 시간: system dynamics의 모델 학습 및 action을 선택하기 위해 optimal control사용
- Global model 및 model-based RL
- Local model 및 model-based RL with constraints
- Uncertainty estimation
- Models for complex observation(e.g., image)
- 만약 policy를 원한다면?
- planning이 아닌 distillation된 policy는 runtime에서 action을 더욱 빠르게 평가.
- Potentially better generalization
- 바로 policy로 backpropate 할 수 있을까?
Today’s Lecture
- 학습된 model을 policy로 backpropagating
- Imitating optimal control과 동일한 이유
- Constrainted optimization formulation
- Guided policy search algorithm
- Imitating optimal control with DAgger
- Model-based vs. model-free RL tradeoffs
- Goals
- Control/ planning으로 guide되는 policy를 학습하는 법 이해.
- 다양한 방법들간의 tradeoff 이해
- Model-based RL으로 policy learning에서 최근 연구의 high-level overview
So how can we train policies?
지금까지 Policy 학습 방법?
- 지금까지의 방법
- Global model 학습(e.g., Gaussian Process, Neural networks)
- Local model 학습 (e.g., linear models)
- But, policy를 사용한다면?
- Replan이 필요없다(faster)
- Potentially better generalization
- Closed loop control
- 아래의 예제와 같은 경우에, prediction을 하지않고 heuristic하게 동작하기도 한다.

Backpropagate directly into the policy?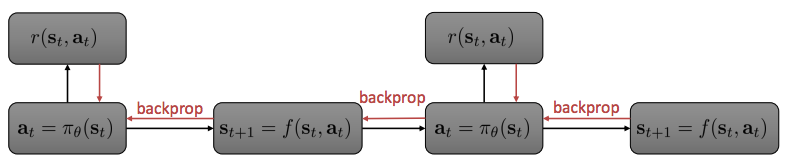

- 문제점:
- Numerical unstable * Backpropagation하게 되면 gradient 값의 변화가 크다.
- Shooting method 이기 때문에 parameter에 대해 high sensitive.
- Policy parameter가 모든 time step과 결합되어 있어, 더이상 2차 LQR와 같은 편리한 방법을 사용하지 못한다(no dynamic programming)
- BPTT(BackPropagation Through Training)으로 long RNNs 학습이 힘든 문제 와 유사
- Vanishing, exploding gradients
- LSTM와 달리 간단한 dynamics를 선택할 수 없다, dynamics는 nature에 의해 선택됨.
- 해결책
- Collocation methods.
- 심지어 더 단순
- Generic trajectory optimization, 다양한 방법으로 풀 수 있음.
- Collocation methods.
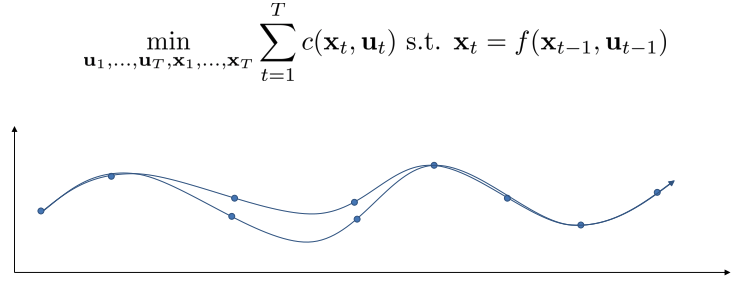
- 어떻게 trajectory optimization에 constraint를 부과할 수 있을까?
- Augmented Lagrangian
Review: dual gradient descent
- Objective function, contraint를 통해 lagragian 을 정의한 후, 이를 미분하여 lagrange multiplier 에 대해 gradient descent를 취해 최적값을 찾는다.
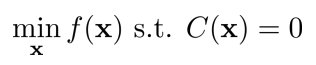
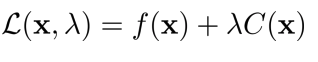
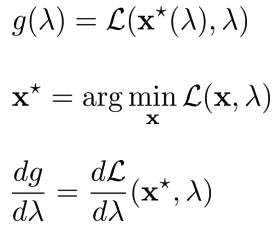
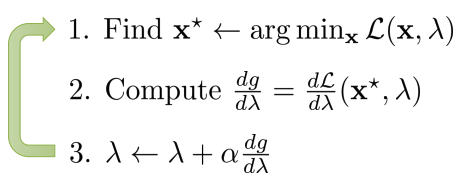
A small tweak to DGD: augmented Lagrangian
- Lagrangian term에 \(p\left \| C \right \|^2\)을 추가(augmented)하여, quadratic term으로 만들고 convexity를 제공하여 더욱 stable 하게 만든다.
- Correct solution으로 여전히 수렴
- Solution과 떨어져 있을 때, quadratic term은 stability를 향상 시키는 경향이 있다.
- Alternating direction method of multipliers(ADMM)과 상당히 유사
Constraining trajectory optimization with dual gradient descent
- Cost function과 \(u = \pi_\theta(x_t)을 constraint로 사용하는 lagrangian으로 정의하면, agmented lagrangian이 만들어지고,\)\lambda$$에 대해 gradient descent를 진행하면, 각각 trajectory(dynamics) 및 policy parameter들이 갱신된다.
- Constrained trajectory optimization method 로 해석될 수 있다.
- Step 2는 supervised learning이므로, optimal control이 expert인 imitation으로 해석 될 수 있다.
- Optimal control “teacher”가 learner를 조정하며 learner가 모방할 수 없는 action은 피한다.
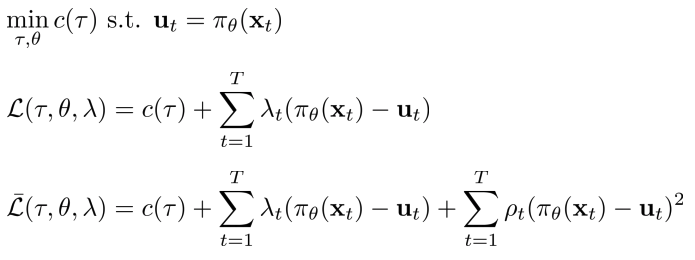
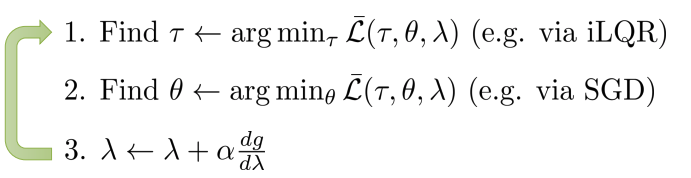
General guided policy search scheme
- Algorithm:
- (어떤)Surrogate cost function에 대해 \(p(\tau)\)(dynamics) 최적화
- (어떤)Supervised objective에 대해 \(\theta\)(policy) 최적화
- Dual variables \(\lambda\) 증강 혹은 변경
- 필요한 정보
- Trajectory form
- Trajectory optimization method
- Surrogate cost fucntion
- Policy에 대한 supervised objective

Deterministic case
Learning with multiple trajectories
Stochastic (Gaussian) GPS
Stochastic (Gaussian) GPS with local models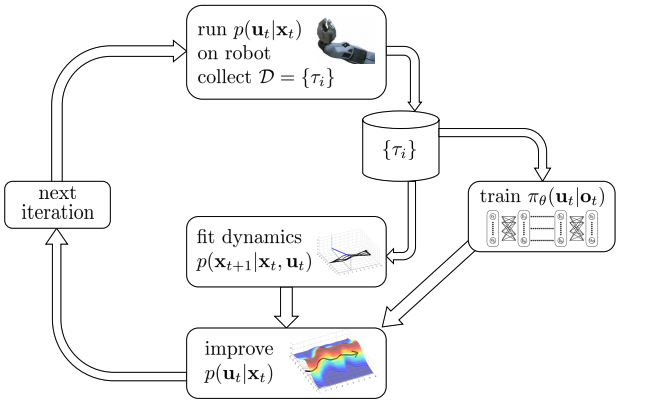
Robotics Example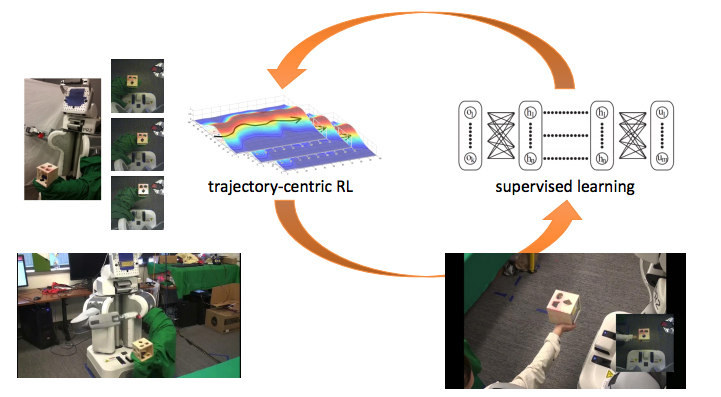
Input Remapping Trick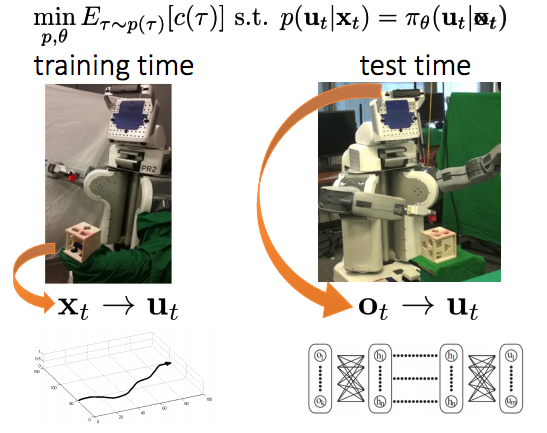
##Imitating optimal control with DAgger##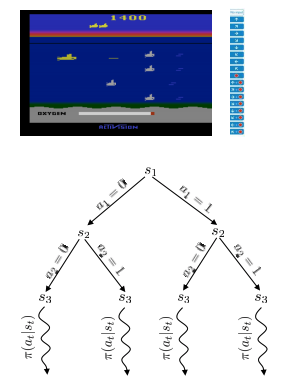
- iLQR(optimal control)이 아닌 MCTS로 대체하지만 step 3에 도입되는 것은 아니다.

A problem with DAgger
- 3번 단계에서 human에게 묻는 것을 computer에게 묻도록 변경 (MCTS 이용)
- 그러나, 문제가 되는 것은 2번 단계.
- 조금 벗어나도 동작이 잘 안되는 문제 발생.


Imitating MPC: PLATO algorithm
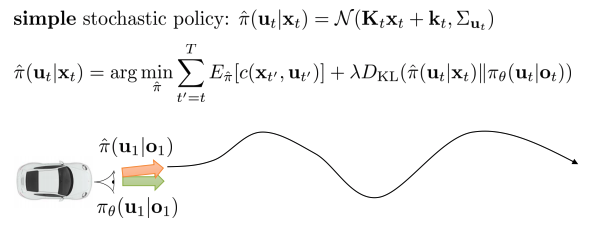

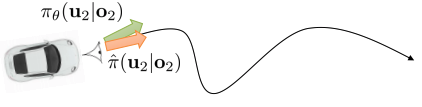
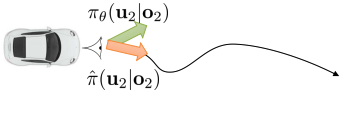
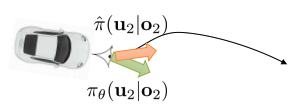
DAgger vs GPS
- Dagger : adaptive expert를 요구하지 않음
- 학습된 policy에서의 state가 label 될 수 있는 한, 모든 expert가 수행할 것.
- 가정: bounded loss까지 expert’s behavior에 매칭이 가능하다
- 항상 가능한 것은 아니다( e.g., partially observed domains)
- GPS : “expert” behavior를 조정
- 초기 expert에서 bounded loss를 요구하지 않음(expert는 변할 것)
Why imitate?
- 상대적으로 stable하고 사용하기 쉽다.
- Supervised learning은 잘 동작
- Control/planning은 (일반적으로) 잘 동작
- 이 두 개의 조합은 (일반적으로) 잘 동작
- Input remapping trick
- raw observation에서 policy를 학습하는 시간에 추가적인 정보의 유용성을 이용할 수 있다
- Policy로 바로 backpropagating 하는 최적화 어려움을 극복
- 일반적으로 sample-efficient하고 실제 물리 시스템에 대해서 실행 가능.
Model-free optimization with a model
- Model을 가지더라도 policy gradient(or 다른 model free RL 방법)을 사용
- Gradient를 사용하는 것보다 때때로 좋음

General “Dyna-style” model-based RL recipe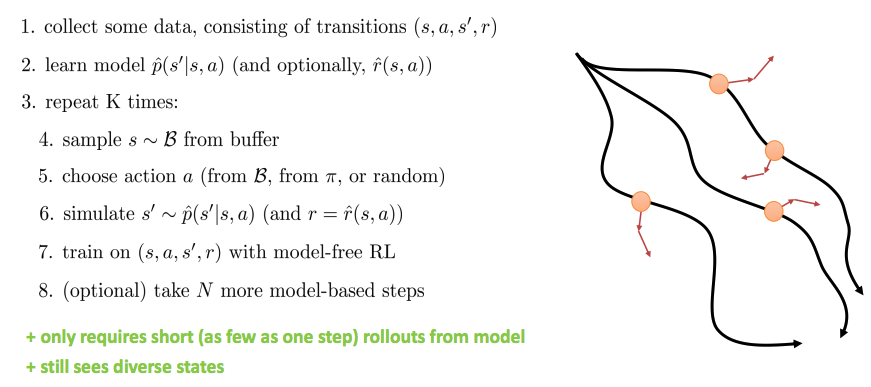
Model-based RL algorithms summary__
- Model 및 plan 학습(without policy)
- 반복적으로 distribution mismatch를 해결하기 위해 더 많은 data 수집
- 약간의 model error를 이동하기 위해 매 time step마다 replan(MPC)
- Policy 학습
- Policy로 backpropagating(e.g., PILCO) - 간단하지만, 잠재적으로 unstable
- constrained optimization framework으로 imitate optimal control (e.g., GPS)
- Dagger-like process를 통한 imitate optimal control (e.g., PLATO)
- model를 가지고 model-free 알고리즘 사용 (Dyna, etc.)
Limitations of model-based RL
- Model의 some kind 요구
- 항상 이용가능하지 않음
- policy보다 학습하는 것이 어려울 수 있음
- Model을 학습하는 것은 시간 및 data가 필요
- 때때로 expressive model classes(neural net)은 빠르지 않음
- 때때로 빠른 모델은 (linear model) expressive 하지 않음
- 추가 가정의 종류
- Linearizability/continuity
- Ability to reset the system (for local linear models)
- Smoothness (for GP-style global models)
- Etc.
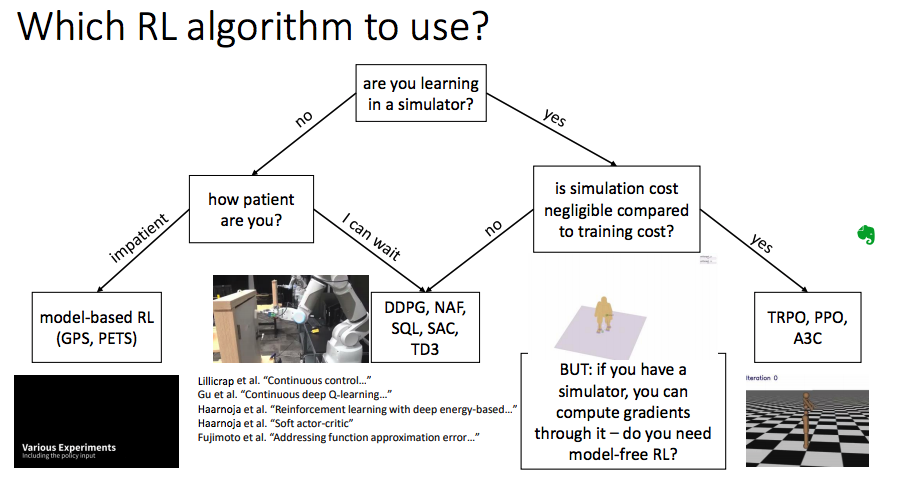
which algorithm do I use?