[CS294 - 112 정리] Lecture4 - Reinforcement Learning Introduction

in Reinforcement learning / Reinforcement learning on Mbrl

Table of Contents

  1. Today’s Lecture
  2. Review
  3. Definitions
  4. The goal of reinforcement learning
  5. Algorithms
  6. Stochastic system
  7. Review
  8. Types of RL algorithms
  9. Reference

Today’s Lecture

  1. Definition of a Markov decision process
  2. Definition of reinforcement learning
  3. Anatomy of a RL algorithm
  4. Brief overview of RL algorithm types
  • Goals:
    • definitions & notation 이해.
    • 중요한 RL 목적 이해.
    • 이용 가능한 알고리즘의 요약.

Review

  • Terminology & notation
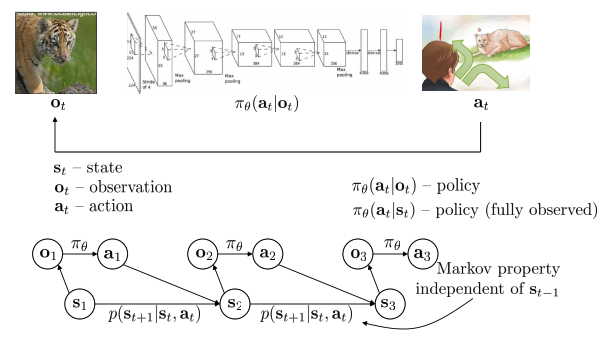
    • Sequential decision making 문제는 observation. action. policy를 포함.
      • Policy 는 조건부 확률 분포이며, 일반적으로 observation이 주어지고 action이 도출된다. 파라미터화되어 있으며, 이 파라미터를 학습시키는 것이 RL의 목적이다. 바로 파라미터를 학습시키는 PG가 있다.
      • 아래의 그래프에서 state 는 Markov property 의미를 만족, observation 은 Markov property를 만족하지 못함.
      • POMDPs과 Fully MDPs가 있는데, 일반적으로 fully MDPs로 가정한다.
An image with a caption
  • Imitation Learning
    • 전문가의 데이터(observation, action)를 수집하고, supervised learning 알고리즘을 사용한다.
      • 위와 같은 behavior cloning접근은 일반적으로 학습이 잘 되지않지만, Dagger를 사용하여 성능을 향상시켰다.
  • Reward functions
    • 전문가의 data가 없는 경우에, 어떻게 하면 효율적으로 policy를 학습할 수 있을까?
    • Reward를 이용하여 action이 좋은지 나쁜지를 찾을 수 있다.
      • Reward는 s, a로 구성, r(s, a)
      • Reward를 순간이 아닌 전체에 걸쳐 최대화 한다.
      • State, action, reward(r(s, a)), transition probability(p(s’\(\mid\)s,a))은 Markov decision process이라 한다.
        • MDP는 기본적으로 RL의 world의 정의.

Definitions

  • Markov chain
    • \(T\) - trainsition operator라고 한다. 현재 state에서 특정한 state로 가는 확률(조건부 확률분포).
      • 왜 operator라고 불리나?
        • Discrete space에서 \(T\) 는 행렬이고, 확률의 vector(\(\mu\))에 대해 operator처럼 행동.
        • p는 state distribution이며, 0보다 큰 값을 가진다.
      • \(T _{i,j}\) matrix는 \(p(s_{t+1} \mid s_t)\), \(s_t\)에서 \(s_{t+1}\)로 전이하며, 간단한 linear equation으로 Markov chain forward \((\overrightarrow{\mu_{t+1}} = T \overrightarrow{\mu_t}\) ) 표현.
    • Continous space에서는 위와 같이 표현하기 어렵지만, computer에서는 기본적인 이론이 위와 같이 정확하게 동일하게 유지된다.
    • Markov property로 인해 \(s_3\)는 \(s_1\)와 독립적.
An image with a caption
  • Markov decision process(MDP)
    • Reward, action 개념 도입.
    • Action, state가 다음 state를 결정.
    • Transition Operator는 tensor(3D) 형태를 가짐.
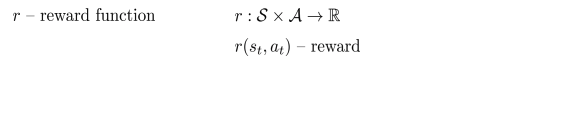
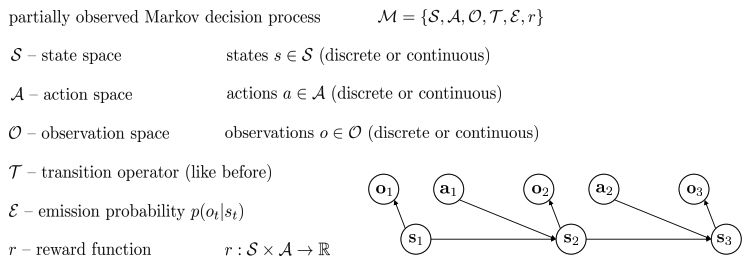
An image with a caption
An image with a caption
  • Partially observed Markov decision process(POMDP)
    • MDP의 generalization model.
    • Observation, emission probability 도입
An image with a caption

The goal of reinforcement learning

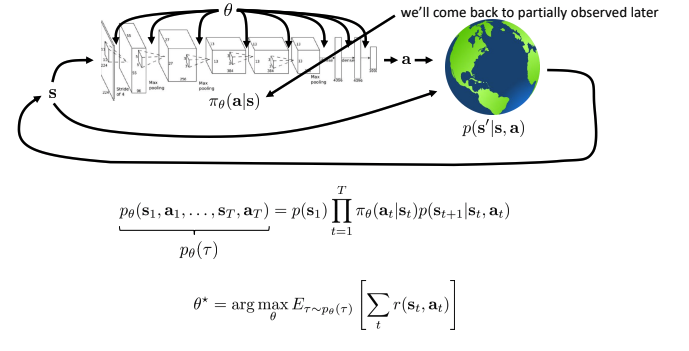
  • 목적:
    • 보상을 최대로하는 policy(π)의 weight(θ)찾기.
    • 파라미터 vector θ* 찾기, trajectory에 걸쳐 보상의 총합의 theta로 유도된 trajectory distribution하에서 expectation의 argmax.
  • \(p(s' \mid s, a)\) 는 일반적으로 모르는 상태이며, 확률이고 다음 state을 지정.
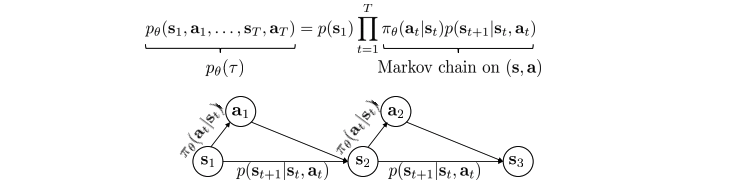
  • Trajectory(sequence, τ)는 state, action으로 구성, chain rule을 이용하여 policy와 transition operator를 product로 표현.
    • Expectation을 사용하는 이유 : parameter vector인 state, action가 random variable이기 때문이고, 여기서의 분포를 사용.
An image with a caption
  • 아래의 항등식이 중요.
    • Markov chain를 분석하는 방법에 사용
    • Stationary distribution 찾는 방법
An image with a caption
An image with a caption

두 MDP 경우를 살펴보자.

  • Finite horizon case: state-action marginal:
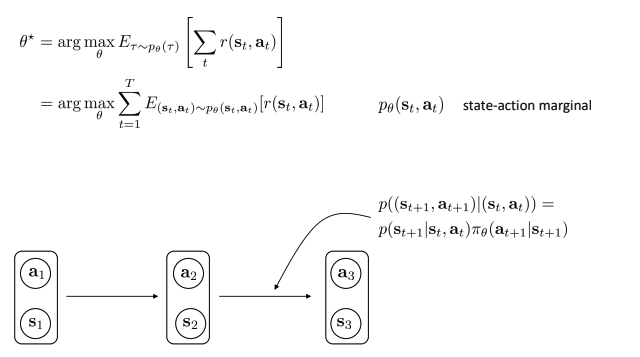
    • Expectation을 내부로 넣으면서, trajectory를 (s, a) pair 로 변경. 실제로 p(s,a)를 아는 것은 힘들지만(나중에 다룸), 매 time step에서 reward를 계산하기 위한 공식을 정의하기 위해 진행.
    • 위에서 언급했듯, \(\tau\) 는 state와 action의 trajectory \(s_1,a_1,…,s_T,a_T\) 인데, Markov chain에서 \(\tau\)는 결국 transition probability 와 policy에 따라 결정.
      • 즉, state-action간의 transition probability 는 \(p((s_{t+1}, a_{t+1}) \mid (s_t, a_t)) = p(s_{t+1} \mid s_t,a_t) \pi_\theta(a_{t+1} \mid s_{t+1})\) 이고, \(p_\theta(s_t, a_t)\) 로 표현 = state-action marginal.
An image with a caption
  • Infinite horizon case: stationary distribution:
    • T가 무한대로 간다면?
      • Mild 가정 아래 Markov chain은 stationary distribution safety를 유도할 수 있다.
        • 안정화시키는 것은 transition인 T가 k step이후에는 우측 하단처럼 될 수 있다.
    • p(s,a)가 stationary distribution에 수렴하는가?
      • Stationary distribution: 시간이 지남에 따라 Markov chain에서 변하지 않은채 남아 있는 확률 분포.
      • Eigen value = 1, mild regularity condition(가벼운 규칙성 조건)에 있음.
      • 결국에 특정값에 수렴 하게 될 것.
An image with a caption
  • 약간 수정됨(T가 무한대로 가기 때문에, T를 나누지만 stationary distribution으로 인해 소거됨)
An image with a caption
  • Expectations and stochastic systems
    • RL에서는, expectation에 대해 항상 고려.
    • Reward function는 not smooth, not differentiable.
      • Expectation을 추가하여 smooth하게 만듬.
An image with a caption

Algorithms

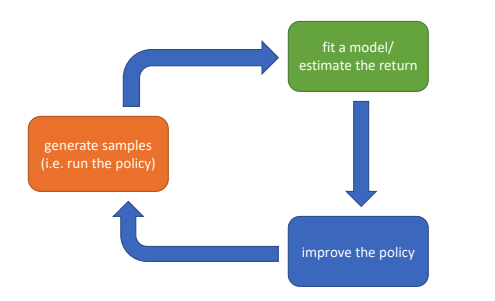
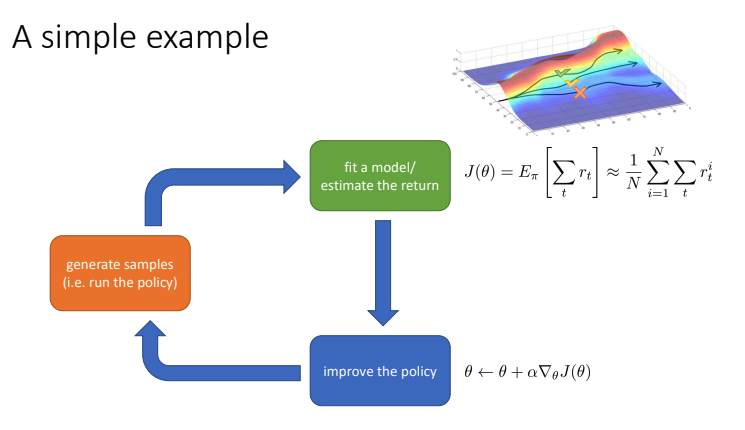
  • RL 알고리즘의 구조
    • Sample 생성(즉, policy를 토대로 agent 행동)
    • Fit a model/ estimate the return(sample들에 대한 평가, return 추정)
    • Policy 향상(policy를 업데이트하는 학습방식)
An image with a caption
  • Policy gradient:
    • Policy를 direct update.
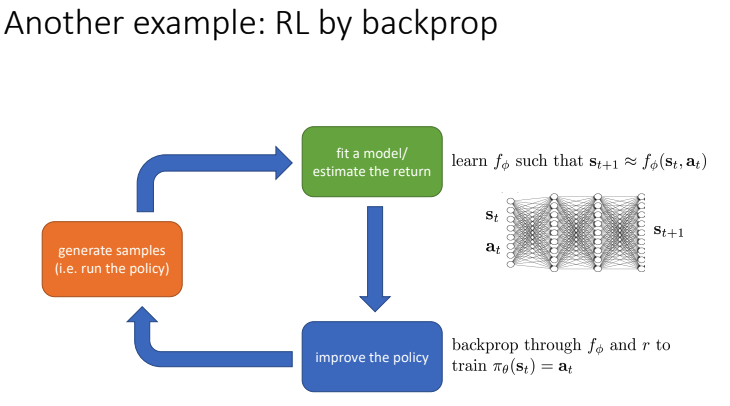
An image with a caption
  • Model based learning:
    • State, action이 들어왔을 때, 다음 state 출력으로 가지는 예측 모델 \(f_\phi\)를 학습한다. \(f_\phi\)가 예측한 다음 state와 실제 다음 state간의 loss를 줄이도록 학습(Model-based RL).
An image with a caption
  • Which parts are expensive?
    • [주황색 박스] : MuJoCo등으로 시뮬레이션을 돌리는 경우는 현실의 시간보다 충분히 빠르게 학습을 돌릴 수 있으므로 큰 문제가 안되지만, 실제로 자율주행이나 로봇 등을 적용할 때 학습하는 경우는 시간이 많이 소요된다.
    • [초록색 박스] : reward를 계산하는 것은 쉽고 빠르게 구현가능하지만, 다음 state를 예측하는 모델 f를 학습하고 최적화하는 것은 오래걸린다. 물론 알고리즘에 따라 다르긴 하다.
    • [파란색 박스] : model f나 reward을 통해 \(\pi_\theta\)를 학습, 알고리즘에 의존.
  • Why is this not enough?
    • 오직 deterministic dynamic, policy만 다룰 수 있다(?).
    • Gradient의 연산을 통해 학습하기 때문에 연속적인 state와 action만 다룰 수 있다.
    • Gradient vanishing 문제 등 최적화에 대한 문제들이 있다.

Stochastic system

  • Stochastic system으로 동작하게 하는 법
    • Conditional expectations
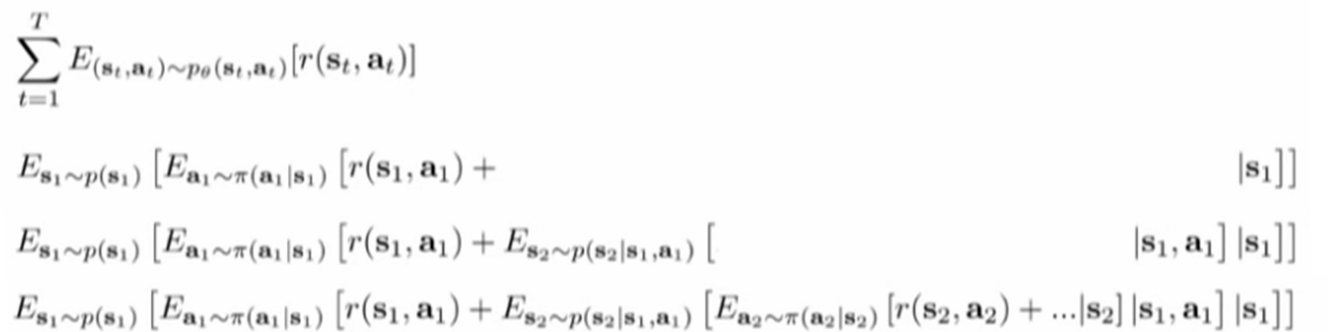
An image with a caption
  • Time step \(T\)까지 진행되고나면 trajectories 따른 reward \(r(s_1,a_1),r(s_2,a_2),r(s_3,a_3)...\) 을 반환받고 그에 맞게 학습.
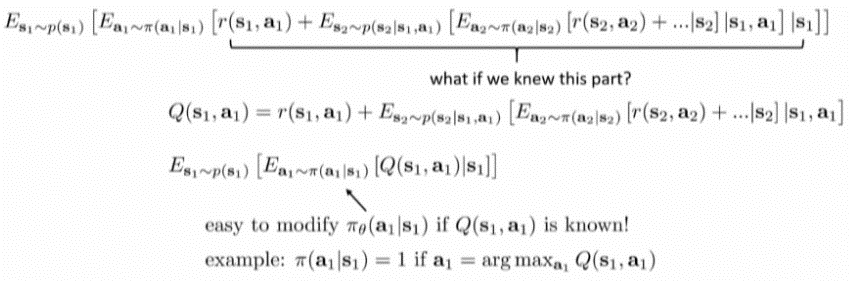
An image with a caption
  • 앞으로 받을 보상을 예측할 수 있다면?
    • time step T까지(trajectory) 기다릴 필요없이 바로 policy를 앞으로의 보상에 맞게 학습 할 수 있을 것이다.
    • 즉, 앞으로의 보상이 최대가 되는 action \(a_1\)이라 할때, policy가 \(a_1\)을 내뱉을 확률을 \(π(a_1 \mid s_1)=1\)이다.
    • 이 때, 앞으로 받을 보상을 예측해주는 함수를 Q-function.
  • Q-function
    • s에서 a를 취해 얻는 전체 보상의 합.
  • Value function
    • s에서 얻는 전체 보상의 합.
    • Q-function으로 표현될 수 있음(V는 모든 action에 대한 Q의 합의 expectation(=average)).
An image with a caption
  • 만약 \(Q_pi(s_t, a_t) > V _\pi (s_t)\)라면, action \(a_t\)는 다른 action들에 비해 평균 이상으로 좋은 action 이다. 이렇게 Q값에 기반해서 더 나은 행동을 하도록 policy를 학습할 수 있는 것이다
    • Idea1: Q를 안다면 policy 향상
      • argmax Q를 이용하여 정책갱신
      • 갱신되는 정책은 무슨 정책이든 상관없이 더 좋아질 것.
    • Idea2: 좋은 행동 a의 확률 증가하기 위한 gradient 계산.
      • Q > V라면 평균보다 좋은 값이다.
      • 따라서, 위의 조건의 action에 대해 probability를 높여주면 된다.
An image with a caption

Review

An image with a caption

Types of RL algorithms

  • Policy gradient: 직접적으로 아래의 목적함수를 미분
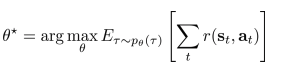
An image with a caption

  • Value-based: (no explicit policy) optimal policy의 value function, Q function을 추정

  • Actor-critic: 현재 policy의 value function, Q function 추정, policy 향상하기 위해 사용

  • Model-based RL: transition model 추정, 그리고

    • planning을 위해 모델사용(no explicit policy)
    • policy 향상을 위해 사용
    • Something else
An image with a caption
An image with a caption
  1. plan하기 위해 모델 사용(no policy)
    1. trajectory 최적화/ 최적 제어(우선적으로 continuous space) - 필수적으로 action에 걸쳐 최적화하기 위해 backpropagation
    2. discrete action space에서 discrete planning - e.g., Monte Carlo tree search
  2. Backpropagate gradient into the policy
    1. 동작하기 위해 몇가지 트릭 필요
  3. Value function을 배우기 위해 모델 사용
    1. DP
    2. Dyna
  • Trade-off
    • 여러가지 강화학습 알고리즘이 있지만, 풀고자 하는 문제의 성격이나 제약조건에 따라 적절한 알고리즘을 선택해야한다. 각각 알고리즘마다 장단점이 있다.
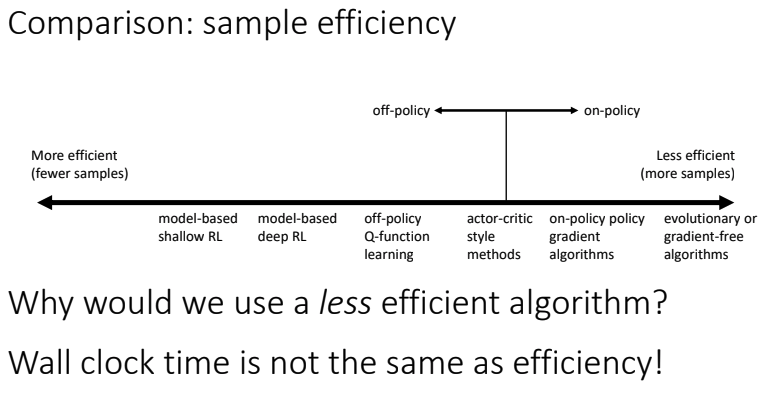
  • Comparison: sample efficiency
    • 샘플 효율성 = 좋은 정책을 얻기 위해서 얼마나 많은 샘플이 필요한가?
    • 가장 중요한 질문: Off policy 알고리즘 ?
      • Off policy: policy에서부터 새로운 샘플 생성없이 policy를 향상할 수 있다.
      • On policy: 각 time마다 약간이라도 policy가 변하면, 새로운 샘플을 생성해야 한다.

More efficient 한 방법이 항상 더 좋은것은 아니다. simulation 비용이 많이 들지 않는다면, less efficient하더라도 더 나은 성능을 위해 많은 sample을 얻어서 학습하는 것이 효율적일 수 있다.

An image with a caption
  • Stability & ease of use
    • 수렴하는지, 어디로 수렴하는지, 항상 수렴하는지에 대한 이슈다.
    • 기존의 supervised learning에서는 gradient descent를 사용하기 때문에 대개 수렴하지만, RL에서는 대체로 gradient descent를 사용하지 않는다.
      • Q-learning: fixed point iteration. 단순한 함수에는 수렴하지만, 복잡한 함수에 수렴하는지는 보장되지 않는다.
      • Model-based RL: model이 reward에 대해 최적화되는 것이 아니다. 그저 다음 state를 예측하기 위해 학습한다. 더 나은 model이 더 나은 policy를 만들어주는지는 보장되어있지 않다.
      • Policy gradient: objective에 대해 직접적으로 gradient descent를 사용하긴 하지만, local optima에 수렴할 가능성이 있다.
An image with a caption

  • Comparison: assumptions

    • Full observation or patially observation?
      • state를 모두 관측할 수 있는 경우(st=ot)가 있고, 부분만 관측 가능한 경우가 있다. 주로 value function fitting에서 full observability를 가정한다.
    • Stochastic or deterministic?
      • Dynamic system 이나 policy에 대한 가정으로, stochastic은 분포를 따르긴 하지만 매번 할 때마다 결과가 달라질 수도 있고, Deterministic은 파라미터가 같다면 같은 입력일때 결과가 매번 같다.
    • Continuous or discrete?
      • Action space나 state space가 연속적인지 불연속적인지에 따라서도 적용하는 알고리즘이 달라진다. 주로 continuous value function learning 이나 model-based RL 에서 continuity나 smoothness를 가정한다.
    • Episodic or infinite horizon?
      • 하나의(finite) episode로 구성되는 환경인지, 시간제약 없이 끝없이 이어지는(infinite) 환경인지에 따라서도 적용하는 알고리즘이 달라진다. 주로 policy gradient나 model-based RL에서 episodic learning을 가정한다.
An image with a caption
An image with a caption

Reference

CS294-112 Lecture4

© 2020. All rights reserved.

Powered by Hydejack v8.1.1