[CS294 - 112 정리] Lecture5 - Policy Gradients Introduction

in Reinforcement learning / Reinforcement learning on Cs294

Table of Contents

  1. Today’s Lecture
  2. Review
  3. Policy gradient
  4. What did we just do?
  5. Reducing variance
  6. On-policy
  7. Reference

Today’s Lecture

  1. The policy gradient algorithm
  2. What does the policy gradient do?
  3. Basic variance reduction: causality
  4. Basic variance reduction: baselines
  5. Policy gradient examples
  • Goals:
    • Understand policy gradient reinforcement learning
    • Understand practical considerations for policy gradients

Review

  • The goal of reinforcement learning
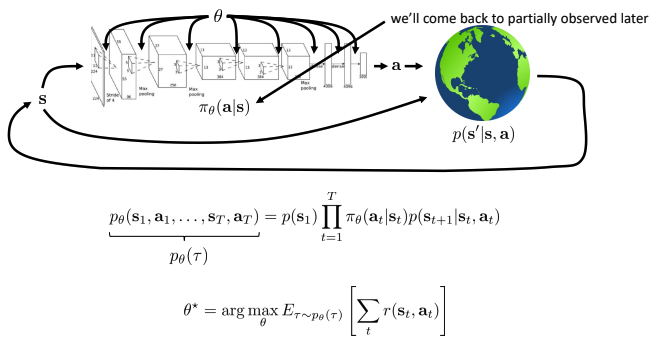
An image with a caption
  • \(\theta^*\)를 찾는 것은 두 가지 경우.
    • Infinite horizon
    • Finite horizon
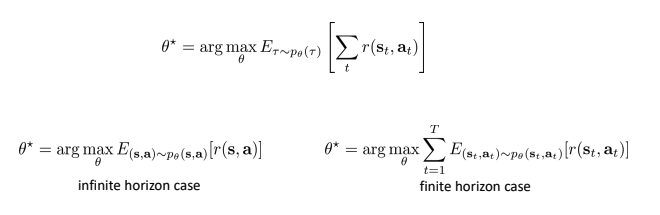
An image with a caption
  • Evaluating the objective
    • 목적(objective function)을 최대화하는 것: trajectory의 총 보상의 합에 대한 기댓 값을 최대화.
      • 실제 값을 구하기 힘들기 때문에, 몬테카를로 기법(=무수히 많은 샘플을 통해 평균값을 구하는 방법)을 이용하여 근사.
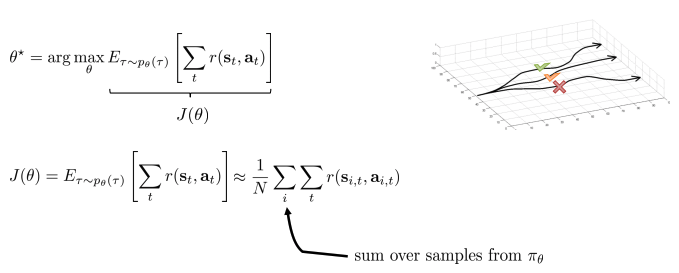
An image with a caption

Policy gradient

  • Direct policy differentiation
    • Policy gradient로 직접 policy의 weight를 갱신.
    • 따라서, objective function을 바로 미분하여 gradient descent 방법을 이용하여 최적점(최소지점)을 찾는다.
      • Log 특성을 사용하여, 미분 및 덧셈 원리 이용하여 단순화 및 tractable하게 변형.
An image with a caption
  • p(s)는 \(\theta\)에 대한 값이 아니므로 미분하면 0.
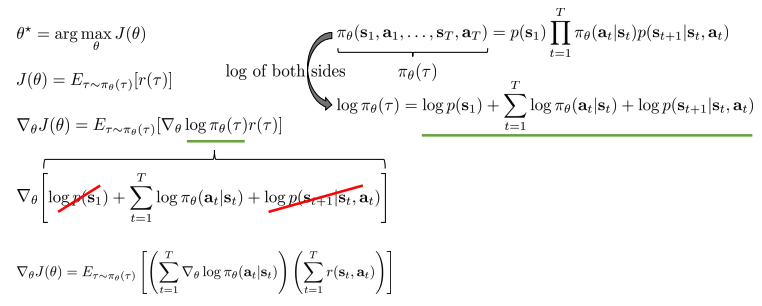
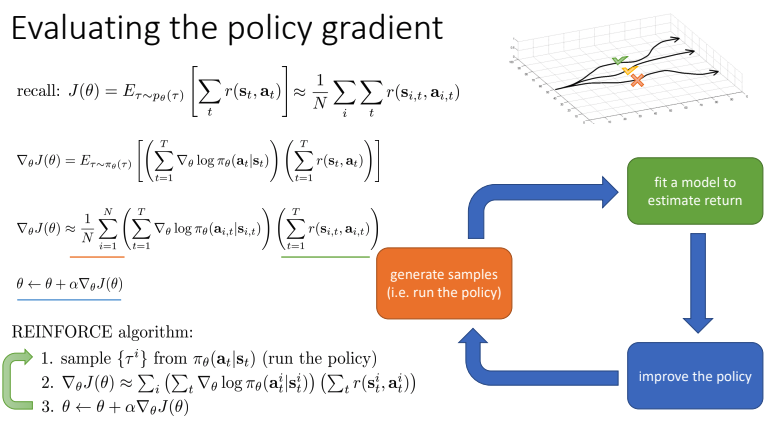
An image with a caption
  • Evaluating the policy gradient
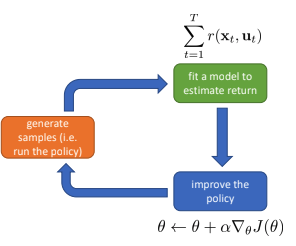
    • REINFORCE 알고리즘:
      • \(1\). policy에 따라 sample 저장 (generate samples)
      • \(2\). objective function을 미분하여 위의 절차(direct policy differentiation)에 따라 policy gradient 계산(fit a model to estimate return)

      • \(3\). gradient descent 방법을 통해 weight 갱신(improve the policy)

      • 그러나, REINFORCE 알고리즘은 잘 동작하지 않는다
        • Variance로 때문, variance reduction을 통해 향상 가능.
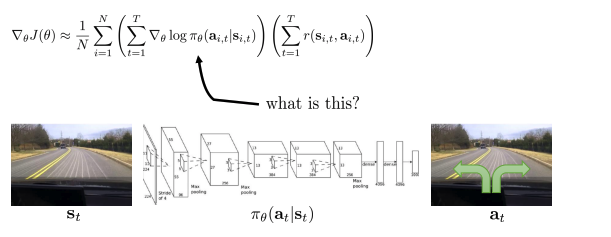
An image with a caption
  • \(Log \pi_\theta\) 는 무엇을 의미?
    • (Imitation learning에서 배웠던) Maximum likelihood 와 상당히 유사
    • 좋은 샘플을 확률 증가, 좋지 않은 샘플은 확률 감소
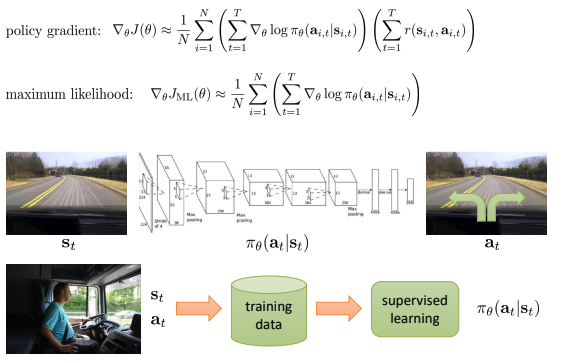
An image with a caption
An image with a caption

What did we just do?

(지금까지 진행사항)

  • Gradient 계산
    • N개의 샘플링(몬테카를로 근사)을 통해 Trajectory 동안의 \(log \pi_\theta\), reward들의 합의 곱으로 표현.
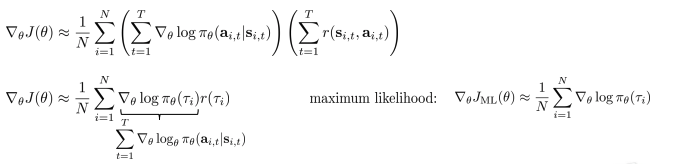
An image with a caption
  • 좋은 것을 더 자주하도록, 나쁜 것을 덜 하도록(maximum likelihood에 유사하기 때문에 \(log \pi_\theta\)가 의미하는 바를 이해할 수 있다) 유도.
  • 간단하게 “trial and error”의 개념을 공식화 한다!
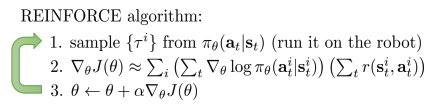
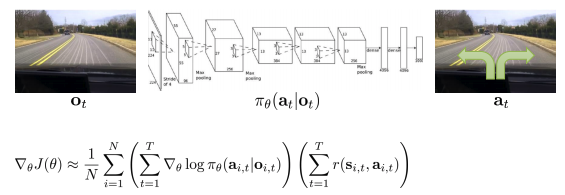
An image with a caption
  • Partial observability
    • Markov property를 실제로는 사용되지 못한다!
    • 수정없이 POMDPs에서 policy gradient를 사용할 수 있다
      • state를 observation으로만 변경.
An image with a caption

What is wrong with the policy gradient?

Policy gradient의 문제는 high variance.

  • 같은 sample을 이용하여도, 학습을 진행하여 추정되는 값의 차이가 크다 - (좋은 직선이 아닌)gradient로 인해 모든 공간에 대해 꿈틀거리게 된다.
  • 많은 이유가 있지만, 하나의 예제만을 설명:
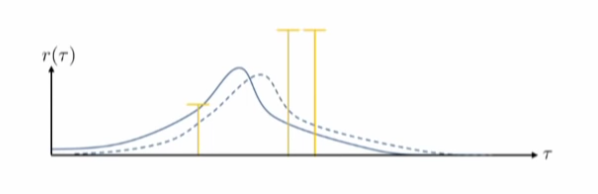
    • 파랑색은 정책에 의한 분포도, 초록색은 세 개의 샘플들(두 개는 작은 positive, 한 개는 큰 negative 값을 가짐)
    • Policy gradient를 통해 policy가 변형.
    • 변경된 점선의 분포도는 다음과 같다.
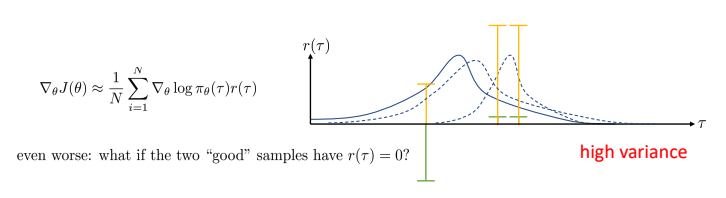
An image with a caption
  • 이상적인 분포도(좋은 것에 대해서는 보상을 주고, 좋지 않은 경우는 피하도록 한다.
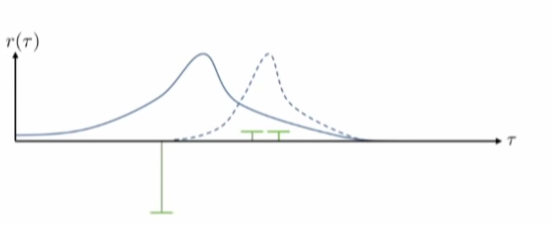
An image with a caption
  • reward function에 상수를 추가하여 더한다면, solution은 이상적이지 않음.
An image with a caption

Review

  • RL 목적함수 평가
    • sample 생성
  • Policy gradient 평가
    • Log-gradient trick
    • sample 생성
  • Policy gradient 이해
    • trial-and-error의 공식화
  • Partial observability
    • 이 조건에서도 잘 동작
  • Policy gradient의 문제
    • Variance
An image with a caption

Reducing variance

  • 첫번째 trick.
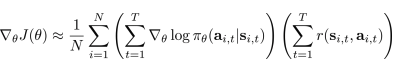
An image with a caption
  • Causality: t < t’ 일때, time t’에서의 policy는 time t에서 reward에 영향을 주지 못한다.
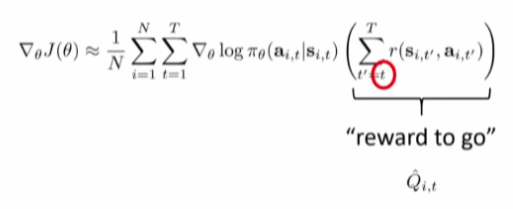
An image with a caption

실제로는 stationary policy가 아니지만(optimal policy는 time varying policy), 제한적이고 간단하게 하기위해 사용하기도 한다.

Baselines

  • 두번째 trick.
An image with a caption
  • Baseline을 사용할 수 있을까? yes, 왜냐하면 unbiased. 아래는 증명.
    • Baseline을 빼는 것은 expectation에서 unbiased.
    • 평균 reward는 최고의 baseline은 아니지만, 꽤 괜찮다.
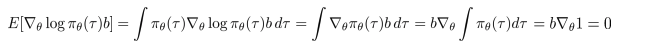
An image with a caption
An image with a caption

Analyzing variance

  • Best baseline
  • 최소(0)이 되는 Variance를 증명(analyzing)할 수 있을까?
    • g = \(∇ \theta log \pi_\theta(\tau)\),
An image with a caption

Review

  • Policy gradient의 문제: high variance
  • 해결책1: Causality 이용
    • 미래는 과거에 영향을 끼치지 못함
  • 해결책2 : Baselines
    • Unbiased!
  • Variance 분석
    • Optimal baseline을 유도

On-policy

Policy gradient: on-policy

  • Neural networks는 각 gradient step에서 약간의 변화만 생김
  • On-policy learning(policy가 변경되면, 새롭게 샘플 생성을 해야함) 은 극단적으로 비효율적일 수 있다.
    • Expectation은 policy에서 sample들을 요구
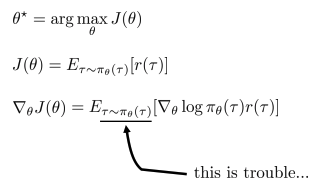
An image with a caption
  • REINFORCE 알고리즘
    • 1번(sampling)을 건너 뛸 수 없음.
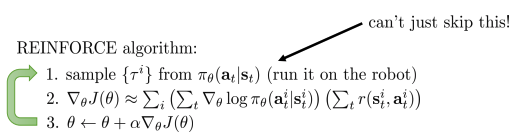
An image with a caption

Off-policy learning & importance sampling

  • 다른 policy의 sample을 가져옴.
  • Importance sampling:
    • 확률 분포의 기대값을 추정하는 기본적인 방법
An image with a caption
  • Importance sampling으로 policy gradient 유도(off-policy policy gradient유도)
    • 새로운 파라미터의 값을 추정할 수 있을까?
      • \(\theta’\)에 대해서만 미분, convenient identity를 사용하여 재정의
    • \(\theta = \theta’\) 일때, 아래와 같이 표현가능,
      • 그렇지 않으면, 틀린 분포로 샘플링.
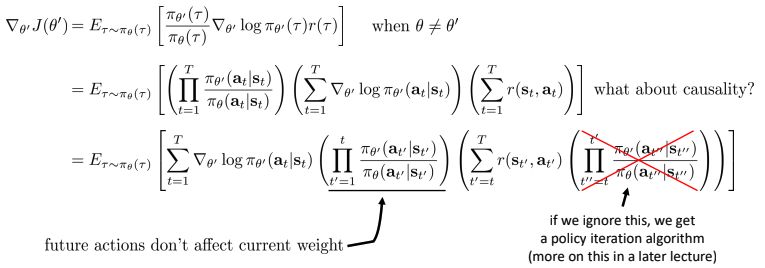
An image with a caption
An image with a caption
  • Off-policy policy gradient:
    • \(\theta\)와 \(\theta’\)가 다를 경우는 다음과 같다
      • 세 개의 term의 곱으로 표현
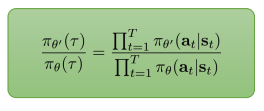
An image with a caption
An image with a caption

Policy gradient with automatic differentiation

  • \(∇\theta log \pi_\theta(a \mid s)\)은 명시적으로 계산하기 위해서는 꽤 비효율적.
  • 어떻게 automatic 미분으로 policy gradient를 계산할 수 있을까?
    • 여기 gradient가 policy gradient를 만족하는 graph가 필요
    • Weighted maximum likelihood와 같은 “pseudo-loss” 를 구현
      • Cross entropy(discrete)
      • Squared error(Gaussian)
An image with a caption

Policy gradient in practice

  • Gradient는 high variance를 가짐
    • 지도학습과 같지는 않음!
    • Gradient는 실제로 noisy할 것!
  • 더 큰 batch 사용을 고려(일반적으로 64많이 사용, but PG는 64000을 사용해야할거임).
  • Learning rate를 보정(tweaking)하는 것은 매우 어렵
    • ADAM은 괜찮음
    • 이후에 고려

Review

  • Policy gradient는 on-policy.
  • Off-policy 변형체로 유도 가능.
    • Importance sampling 사용
    • T만큼 지수승
    • state 부분은 무시 할 수 있다(approximation)
  • 자동적 미분으로 구현 가능
    • Backpropagate가 무엇인지 알아야 한다.
  • 실전에서 고려
    • batch size, learning rates, optimizers

Reference

CS294-112 Lecture5

© 2020. All rights reserved.

Powered by Hydejack v8.1.1