Robot Dynamics & control: Lecture 3 - Forward Kinematics: The Denavit-Hartenberg Convention

in Robotics / Robotics & Control on Robotics

Table of Contents

  1. Introduction
  2. Kinematic Chains
  3. Denavit - Hartenberg Representation

Introduction

  • The forward kinematics problem is to determine the position and orientation of the end-effector, given the values for the joint variables of the robot.
  • The joint variables: angle between the links for revolute or rotational joint link extension for the prismatic or sliding joint.
\[\begin{aligned} \begin{bmatrix} x \\ y \\ z \\ \psi \\ \theta \\ \phi \\ \end{bmatrix} = f(\theta_1, \cdots , \theta_n, d_1 , \cdots , d_n) \end{aligned}\]
  • \(f\): forward kinematics

Kinematic Chains

  • A robot manupulator n joints will have n+1 links including ground.
  • Joint number: 1 ~ n, Link number: 0 ~ n
  • Joint i connects link i-1 to link i.
  • Joint i is fixed at link i-1, so when joint i is actuated, link i moves.
  • Link 0(the first link) is fixed and does not move when the joints are actuated.
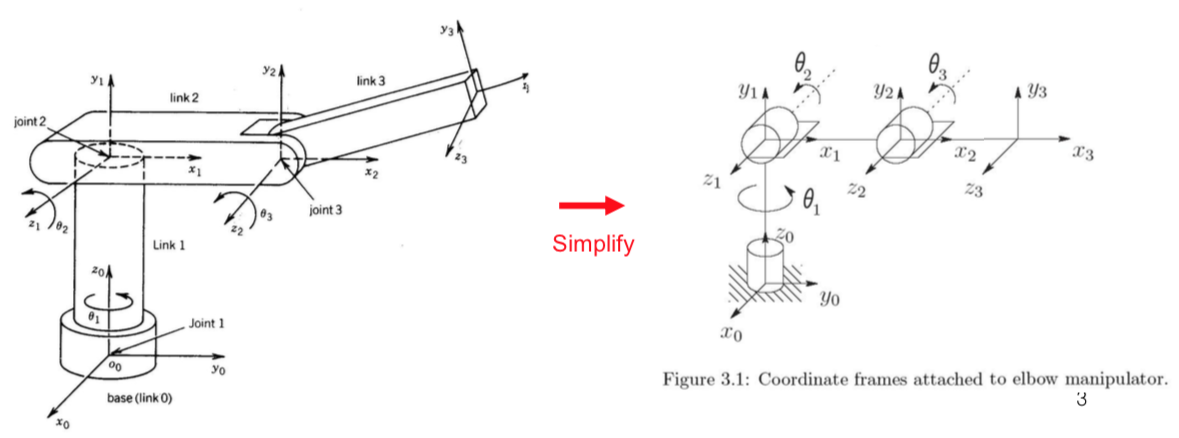
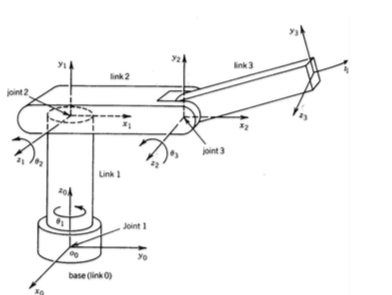
An image with a caption
  • With the i^{th} joint, we associate a joint variable, denoted by q_i.
    • \(\theta_i\): joint \(i\) revolute
    • \(d_i\): joint \(i\) prismatic
  • \(o_i x_i y_i z_i\) is attached to link i \(\rightarrow\) when joint i is actuated, link i and its attached frame \(o_i x_i y_i z_i\) experience a resulting motion.
  • The frame \(o_0 x_0 y_0 z_0\) which is attached to the robot base, is referred to as the inertial frame(=world coordinate).
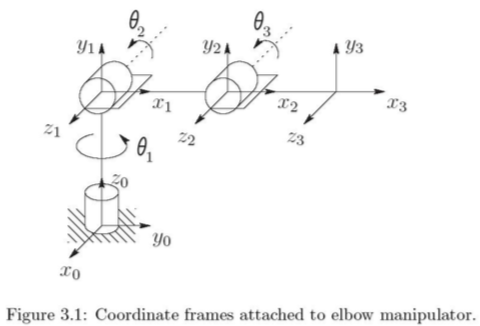
An image with a caption
  • Suppose \(A_i\) is the homogeneous transformation matrix that expresses the position and orientation of \(o_i x_i y_i z_i\) with respect to \(o_{i-1} x_{i-1} y_{i-1} z_{i-1}\).
  • The matrix \(A_i\) is not constant but varies as the configuration of the robot is changed, and \(A_i\) is a function of only a single joint variable, namely \(q_i\).
\[\begin{aligned} A_i = A_i (q_i) \end{aligned}\]
  • Homogeneous transformation matrix \(T^i_j\) that expresses the position and orientation of \(o_j x_j y_j z_j\) with respect to \(o_i x_i y_i z_i\) .
\[\begin{aligned} T^i_j = A_{i+1} A_{i+2} \cdot A_{j-1} A_{j} \qquad if \quad i < j \\ T^i_j = I \qquad if \quad i = j \\ T^i_j = (T^j_i)^{-1} \qquad if \quad i > j \end{aligned}\]
  • The homogeneous transformation matrix denoted by the position(\(o^0_n\)) and orientation (\(R^0_n\)) of the end-effector with respect to the inertial or base frame:
    • This is forward kinematics!
    • But, it is possible to achieve a considerable amount of stream linking and simplication by introducing D-H representation.
\[\begin{aligned} H &= \begin{bmatrix} R^0_n & o^0_n\\ 0 & 1 \\ \end{bmatrix} \\ &= T^0_n \\ &= A_1(q_i) \cdot A_n(q_n) \end{aligned}\]
  • Each homogeneous transformation matrix:
\[\begin{aligned} A_i &= \begin{bmatrix} R^{i-1}_i & o^{i-1}_i\\ 0 & 1 \\ \end{bmatrix} \end{aligned}\]
  • Hence,
\[\begin{aligned} T^i_j &= A_{i+1} \cdots A_j &= \begin{bmatrix} R^{i}_j & o^{i}_j\\ 0 & 1 \\ \end{bmatrix} , R^i_{j} &= R^i_{i+1} \cdots R^{j-1}_j \\ o^i_{j} &= o^i_{j-1} + R^i_{j-1} o^{j-1}_j \end{aligned}\]
  • It is possible to carry out all of the analysis using an arbitrary frame attached to each link.
  • However, it is helpful to be systematic in the choice of these frames by using the Denavit-Hartenberg, or D-H convention.
  • In D-H convention, each homogeneous tranformation matrix \(A_i\) is represented as a product of four basic transformations.

Denavit - Hartenberg Representation

\[\begin{aligned} A &= Rot_{z, \theta_i} Trans_{z, d_i} Trans_{x, a_i} Rot_{x, \alpha_i} \\ &= \begin{bmatrix} c_{\theta_i} & -s_{\theta_i} & 0 & 0\\ s_{\theta_i} & c_{\theta_i} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & d_i\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & a_i\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & c_{\alpha_i} & - s_{\alpha_i}& 0\\ 0 & s_{\alpha_i} & c_{\alpha_i}& 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ &= \begin{bmatrix} c_{\theta_i} & -s_{\theta_i}c_{\alpha_i} & s_{\theta_i}s_{\alpha_i} & \alpha_i c_{\theta_i}\\ s_{\theta_i} & c_{\theta_i}c_{\alpha_i} & -c_{\theta_i}s_{\alpha_i} & \alpha_i s_{\theta_i}\\ 0 & s_{\alpha_i} & c_{\alpha_i}& d_i\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{aligned}\]
  • Since the matrix A_i is a function of a single variable, the 3 of the 4 quantities are constant for a given link.
    • \(d_i\): Joint variable for a prismatic joint.
    • \(\theta_i\): Joint variable for a revolute joint.

  • By a clever choice of the origin and coordinate axes, it is possible to cut down the number of parameters and needed from 6 to 4.

  • Existence and uniqueness issues:
    • Clearly, it is not possible to represent any arbitrary homogeneous transformation using only four parameters
    • But, is is possible to derive a unique homogeneous transformation matrix \(A\) under the following two conditions.

DH1) The axis \(x_1\) is perpendicular to the axis \(z_0\).

DH2) The axis \(x_1\) intersects the axis \(z_0\)

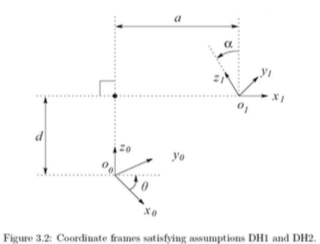
An image with a caption
  • Under DH1 and DH2, we claim that there exist unique numbers \(a, d, \theta , \alpha\) such that.
    • \[A = Rot_{z,\theta} Trans_{z,d} Trans_{x,a} Rot_{x, \alpha}\]
  • Physical interpretation of four quantities:
    • a: Distance between the axes \(z_0\) and \(z_1\) measured along the axis \(x_1\)
    • d: Distance between the origin \(o_0\) and the intersection of the \(x_1\) axis with \(z_0\) measured along the \(z_0\) axis.
An image with a caption
  • Physical interpretation of 4 quantities:
    • \(\alpha\): Angle between the axes \(z_0\) and \(z_1\) measured in a plane normal to \(x_1\).
    • \(\theta\): Angle between \(x_0\) and \(x_1\) measured in a plane normal to \(z_0\).
An image with a caption
  • Assigning the coordinate frames
    • For a given robot manipulator, one can always choose the frame 0, 1, …, n in such a way that the DH1 and DH2 are satisfied.
    • It is important to keep in mind that the choices of the various coordinate frames are not unique, even when constrained by the DH1 and DH2.
    • However, it is important to note that the end result(\(T^0_n\)) will be the same, regardless of the assignment if untermediate link frames .
  • We assign \(z_i\) to be the axis of actuation for joint i+1
    • If joint i+1 is revolute, \(z_i\) is the axis of revolution of joint i+1.
    • If joint i+1 is prismatic, \(z_i\) is the axis of translation of joint i+1.
An image with a caption
  • In order to set up frame i it is necessary to consider 3 cases:
  • case 1:
    • \(z_{i-1}\) and \(z_i\) are not coplanar:
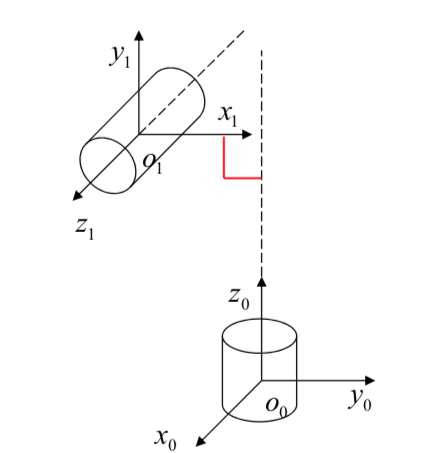
An image with a caption
  • case 2:
    • \(z_{i-1}\) is parallel to \(z_i\):
      • \(d_i, \alpha_i\) are 0 in this case
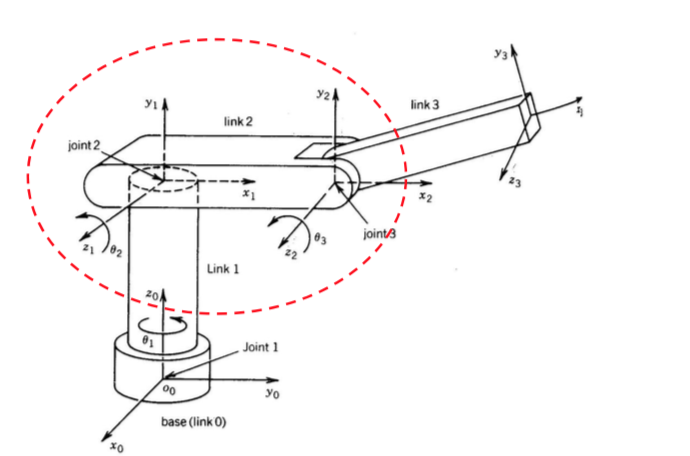
An image with a caption
  • case 3:
    • \(z_{i-1}\) intersects \(z_i\):
      • \(a_i\) are 0 in this case
An image with a caption
  • This constructive procedure works frame 0, …, n-1 in an n-link robot.
  • The final coordinate system \(o_n x_n y_n z_n\) is commonly referred to as the end-effctor(or tool frame)
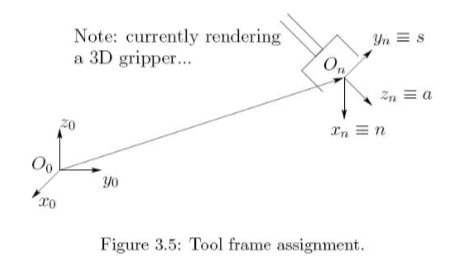
An image with a caption

  • Terminology arises from the fact that the direction a is the approach direction, the s direction is the sliding direction, and n is the direction normal to the plane formed by a and s.

  • Note the following important fact:
    • The quantities \(a_i\) and \(\alpha\) are always constant (characteristics of the manipulator)
    • If joint i is prismatic, then \(\theta_i\) is also a constant, while \(d_i\) is the \(i^{th}\) joint variable.
    • If joint i is revolute, then \(d_i\) is also a constant, while \(\theta_i\) is the \(i^{th}\) joint variable.
  • Summary:

\(1.\) Locate and label the joint axes \(z_0, ..., z_{n-1}\).

\(2.\) Establish the base frame. Set the origin anywhere on the \(z_0\)-axis. The \(x_0\) and \(y_0\) axed are chosen conveniently to form a right-hand frame. For i = 1, …, n-1, perform step 3 to 5.

\(3.\) If \(z_i\) intersects \(z_{i-1}\), locate \(o_i\) at this intersection. If \(z_i\) and \(z_{i-1}\) are parallel, locate \(o_i\) in any convenient position along \(z_i\).

\(4.\) Establish \(x_i\) along the common normal between \(z_{i-1}\) and \(z_i\) through \(o_i\), or in the direction normal to the \(z_{i-1} - z_i\) plane if \(z_{i-1}\) and \(z_i\) intersect.

\(5.\) Establish \(y_i\) to complete a right-hand frame

\(6.\) Establish the end-effector frame \(o_n x_n y_n z_n\). Assuming the n-th joint is revolute, set \(z_n\) = a along the direction \(z_{n-1}\). Establish the origin on conveniently along \(z_n\), preferably at the center of the gripper or at the tip of any tool. Set \(y_n\) = s in the direction of the gripper closure.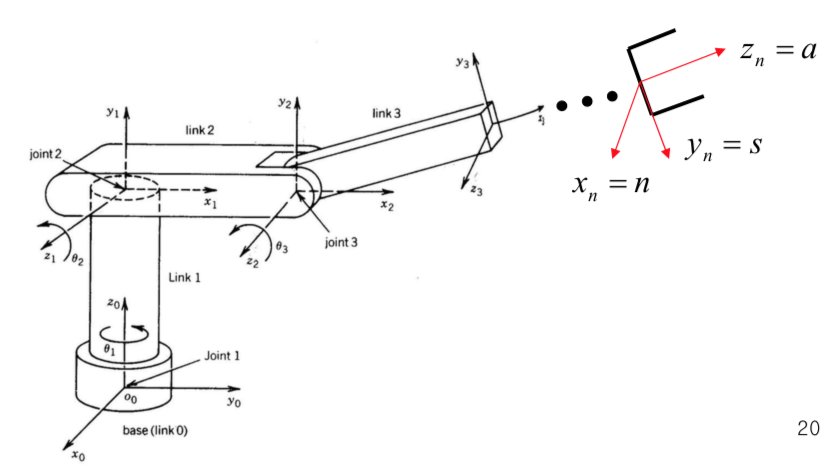

An image with a caption

\(7.\) Create a table of link parameters \(a_i, \alpha_i , d_i, \theta_i\).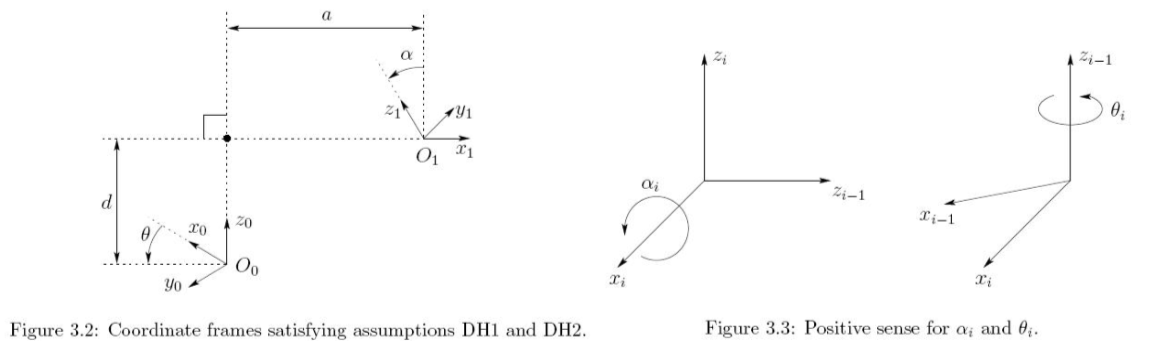

An image with a caption

\(8.\) From the homogeneous transformation matrices \(A_i\) by substituting the above parameters into \[\begin{aligned} A &= Rot_{z, \theta_i} Trans_{z, d_i} Trans_{x, a_i} Rot_{x, \alpha_i} \\ &= \begin{bmatrix} c_{\theta_i} & -s_{\theta_i}c_{\alpha_i} & s_{\theta_i}s_{\alpha_i} & \alpha_i c_{\theta_i}\\ s_{\theta_i} & c_{\theta_i}c_{\alpha_i} & -c_{\theta_i}s_{\alpha_i} & \alpha_i s_{\theta_i}\\ 0 & s_{\alpha_i} & c_{\alpha_i}& d_i\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \end{aligned}\]

\(9.\) Form \(T^0_n = A_1 \cdots A_n\). This then gives the position and orientation of the tool frame expressed in base coordinates.

Reference:

© 2020. All rights reserved.

Powered by Hydejack v8.1.1