Robot Dynamics & control: Lecture 1 - Introduction

02 Mar 2018 in Robotics / Robotics & Control on Robotics

Table of Contents

1. Components & Structure of Robots:
   1. Degrees of Freedom
   2. Workspace
   3. Common Kinematic Arrangements
      1. Articulated configuration(RRR)
      2. Spherical Configuration(RRP)
      3. SCARA Configuration(RRP)
      4. Cylindrical Configuration(RPP)
      5. Cartesian Configuration(PPP)
      6. Parallel manupulator
   4. Wrists and End-Effectors
2. Problem 1: Forward Kinematics
   1. Forward kinematic equations
      1. Tool(End-effector) position
      2. Tool(End-effector) Orientation
3. Problem 2: Inverse Kinematics
   1. Law of Cosines
   2. Inverse kinematic equations.
   3. Another way - Closed form
   4. Another way - Numerical Solution
4. Problem 3: Velocity Kinematics
5. Problem 4: Path Planning and Trajectory Generation
   1. Path planning
   2. Trajectory Generation:
6. Problem 5: Dynamics
   1. Example 1: Three link-revolute arm
7. Problem 6: Position Control
   1. Example: Independent Joint Position Control
8. Problem 7: Force Control

Components & Structure of Robots:

• Robot manipulators are composed of links connected by joints into a kinematic chain.
  • Revolute joint: allows relative rotation between two links.
  • Prismatic joint: allows a linear relative motion between two links.

Degrees of Freedom

• The number of joints determines the DOF of the manipulator.
• A typical manipulator should possess at least six independent DOF:
  • Three for positioning + Three for orientation.
• With fewer than six DOF the arm cannot reach every point in its work encironment with arbitray orientation.

Workspace

• The total volume swept out by the end-effector as the manipulator executes all possible motions.
• Reachable workspace : entire set of points reachable by the manipulator
• Dextrous workspace: subset of the reachable workspace that the manipulator can reach with an arbitrary orientation of the end-effector.

Common Kinematic Arrangements

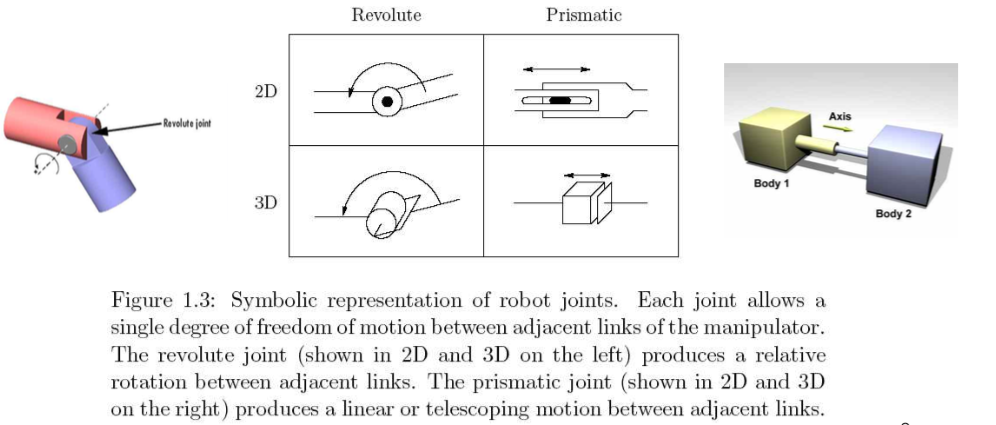
Articulated configuration(RRR)

• This configuration provides for relatively large freedom of movement in a compact space
• The links and joints are analogous to human joint.

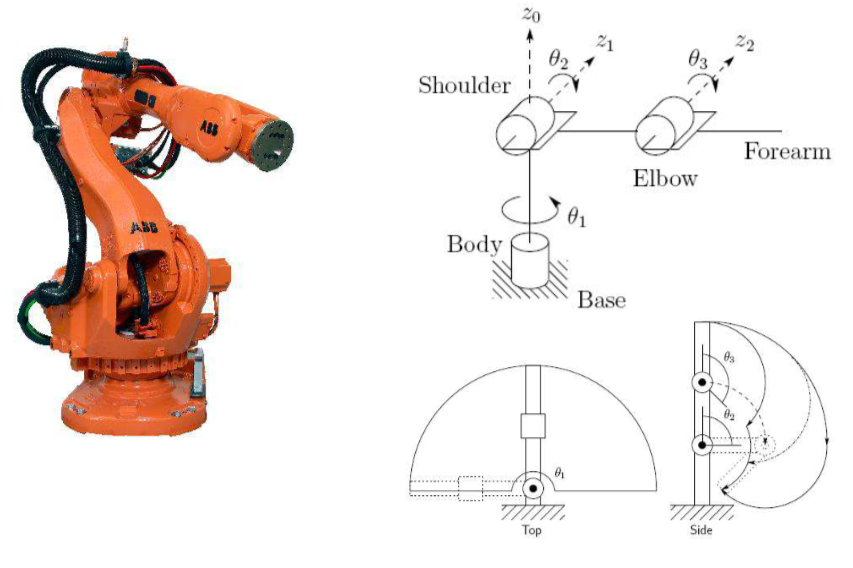
Spherical Configuration(RRP)

• The third joint of the articulated robot is replaced by a prismatic joint.
• The ‘Stanford-arm’ is an example of a spherical manupulator.

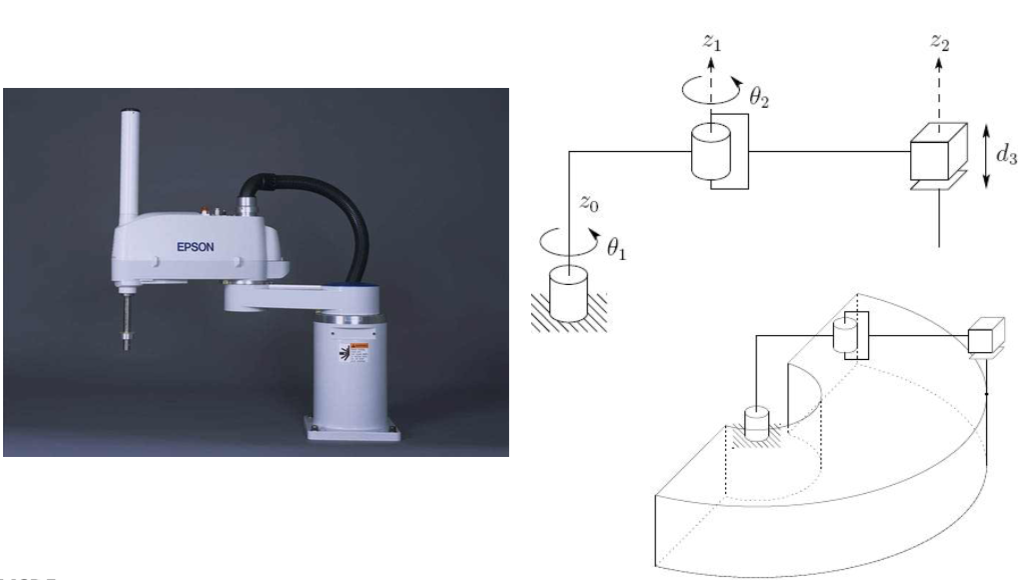
SCARA Configuration(RRP)

• The so-called SCARA(Selective Compliant Articulated Robot for Assembly) has \(z_0, z_1, z_2\) prallel.
• Ideal for table top assembly such as pick and place task.

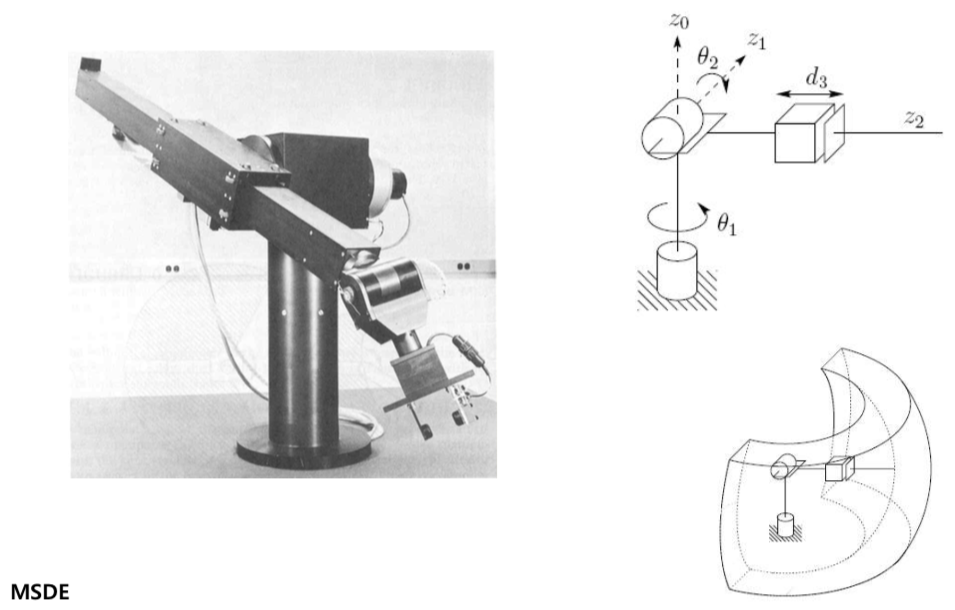
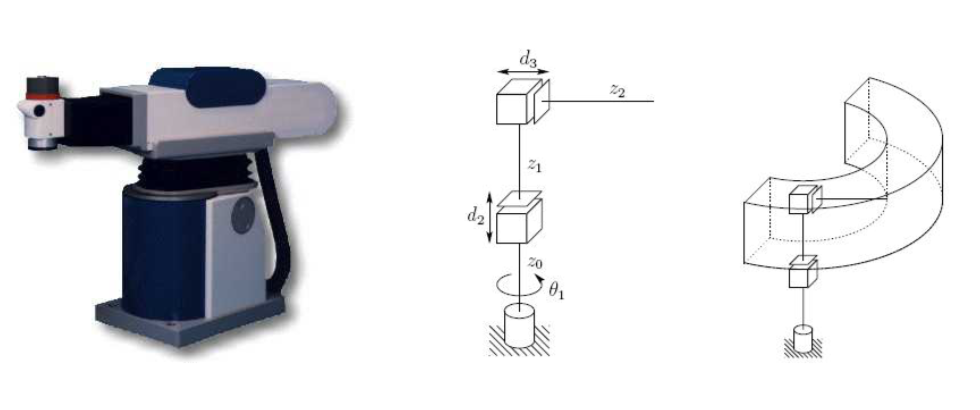
Cylindrical Configuration(RPP)

• The first joint is revolute, while the second and third joints are prismatic.
• This is often used in materials transfer task.

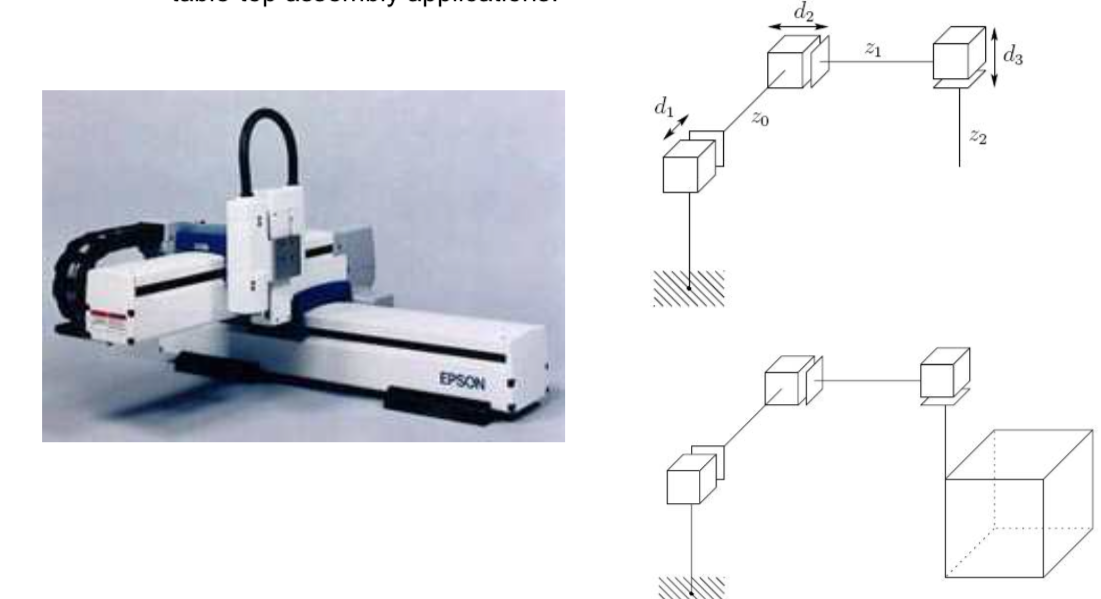
Cartesian Configuration(PPP)

• The configuration is useful for table-top assembly applications.
• This is often used in pick and place operations.

Parallel manupulator

• The configuration forms a closed chain by using several independent kinematic chains connecting the vase to the end-effector.
• The closed chain results in greater structural rigidity.
• This robot generally have much structural rigidity than serial link robots.

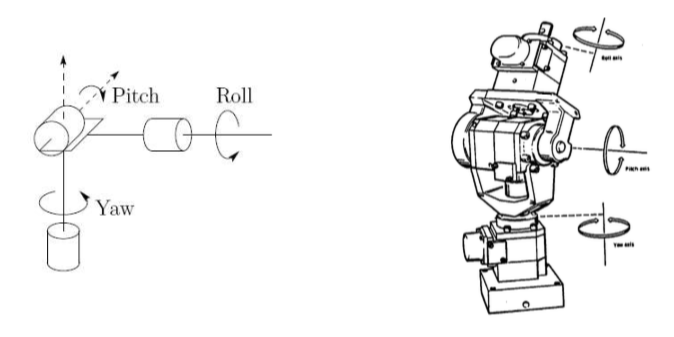
Wrists and End-Effectors

• The wrist of a manipulator refers to the joints in the kinematic chain berween the arm and hand.
• It is increasingly common to design manipulators with spherical wrists, by which we mean wrists whose three joint axes intersect at common point.
• 6 DOF = 3 DOF for wrist + 3DOF for arm
• The arm and wrist assemblies are used primarily for positioning the end-effector(=hand)
• The simplest type of end-effector are grippers.

---

Problem 1: Forward Kinematics

• The first problem is to describe position and orientation of the tool.
• Determination of the position and orientation of the end-effector(or tool) in terms of joint variables(angle or displacement).

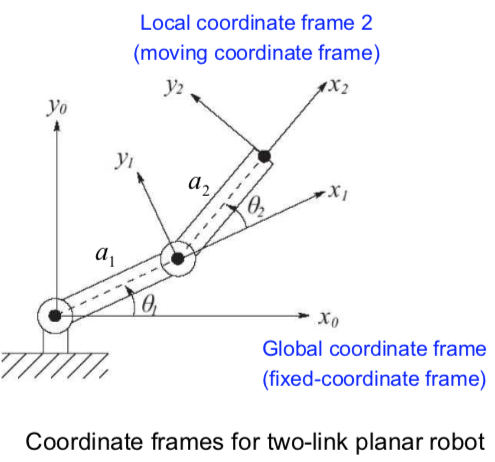
Forward kinematic equations

Tool(End-effector) position

\(\begin{aligned} \qquad x = a_1 cos \theta_1 + a_2 cos( \theta_1 + \theta_2) \\ \qquad y = a_1 sin \theta_1 + a_2 sin( \theta_1 + \theta_2) \end{aligned}\)

Tool(End-effector) Orientation

Rotation matrix: \(\begin{aligned} \qquad \begin{bmatrix} i_2 \cdot i_0 & j_2 \cdot i_0 \\ i_2 \cdot j_0 & j_2 \cdot j_0 \end{bmatrix} &= \begin{bmatrix} cos(\theta_1 + \theta_2) & -sin(\theta_1 + \theta_2) \\ sin(\theta_1 + \theta_2) & cos(\theta_1 + \theta_2) \end{bmatrix} \end{aligned}\)

Note: Denavit-Hartenberg Convention & Homogeneous transformation is needed to express these relationship.

---

Problem 2: Inverse Kinematics

• In order to command the robot to move to arbitrary position, we need the joint variables in terms of x and y coordinates.
  • we may need the forward kinematic equations in advance.
• Since the forward kinematic equations are nonlinear, a solution may not be easy.
• There may be many solutions or infinite number of solution.
  • we can impose constraints.

Law of Cosines

\[\begin{aligned} & cos \theta_2 = \frac{x^2 + y^2 - a_1 ^2 - a^2 _2}{2 a_1 a_2} &\cong D \\ & \therefore \theta _2 = cos ^{-1}(D) \end{aligned}\]

• Not better way.
• This can not distinguish the elbow up and down.

\[\begin{aligned} & sin ^2 \theta _2 + cos ^2 \theta_2 = 1 \rightarrow sin \theta _2 = \pm \sqrt{1 - D^2} \\ & \therefore \theta _2 = tan ^{-1} (\frac{1 - D^2}{D}) \end{aligned}\]

• Signs determine the elbow up and down.

Inverse kinematic equations.

\[\begin{aligned} & \theta _2 = tan ^{-1} \frac{\pm \sqrt{1 - D ^2}}{D} \\ & \theta _1 = tan ^{-1} (\frac{y}{x}) - tan ^{-1}(\frac{a_2 sin \theta _2}{a_1 + a_2 cos \theta_2}) \end{aligned}\]

• For verification, we can check using the Forward Kinematics(cross-check)

Another way - Closed form

• Closed form: \(\theta_1, \theta_2\) is expressed with x, y using forward kinematics.

  • x, y를 제곱하여 \(cos \theta_2, sin \theta_2\)을 얻은 후, \(\theta_2\)를 구한다.

\[\begin{aligned} & x = a_1 cos \theta_1 + a_2 cos(\theta _1 + \theta _2) \\ & y = a_1 sin \theta_1 + a_2 sin(\theta _1 + \theta _2) \\ & \qquad \qquad \qquad \triangledown \\ \\ x^2 &= a^2 _1 cos ^2 \theta_1 + a^2_2 cos^2 (\theta_1 + \theta_2 ) + 2 a_1 a_2 cos \theta_1 cos(\theta_1 + \theta_2)\\ & = a^2 _1 cos ^2 \theta_1 + a^2_2 cos^2 (\theta_1 + \theta_2 ) + a_1 a_2 (cos (2 \theta_1 + \theta_2) + cos\theta_2)\\ y^2 &= a^2 _1 sin ^2 \theta_1 + a^2_2 sin^2 (\theta_1 + \theta_2 ) + 2 a_1 a_2 sin \theta_1 sin(\theta_1 + \theta_2)\\ & = a^2 _1 sin ^2 \theta_1 + a^2_2 sin^2 (\theta_1 + \theta_2 ) - a_1 a_2 (cos (2 \theta_1 + \theta_2) - cos\theta_2)\\ & \qquad \qquad \qquad \triangledown \\ \\ & x^2 +y^2 = a^2_1 +a^2 _2 + 2a_1 a_2 cos \theta_2 \\ & \qquad \qquad \qquad \triangledown \\ \\ & cos \theta_2 = \frac{x^2 + y^2 - a_1 ^2 - a^2 _2}{2 a_1 a_2} \quad \cong D \\ & sin \theta_2 = \pm \sqrt{1 - D^2} \\ \\ & \therefore \theta_2 = tan ^{-1} (\frac{\pm \sqrt{1-D^2}}{D}) \end{aligned}\]

• 아래의 식(1)을 얻기 위해 \(cos \theta_1, sin\theta_2\)를 각각 곱하고, 아래의 식(2)을 얻기 위해 \(sin \theta_1, cos \theta_1\)를 각각 곱한다.
• 이 후 x, y를 곱하여 더하rh 빼서 \(cos \theta_1,sin \theta_1\)를 얻어 \(\theta_1\) 을 구한다.

\[\begin{aligned} & x = a_1 cos \theta_1 + a_2 cos(\theta _1 + \theta _2) \\ & y = a_1 sin \theta_1 + a_2 sin(\theta _1 + \theta _2) \\ \\ & x cos \theta_1 = a_1 cos ^2 \theta_2 + a_2 cos \theta_1 (cos \theta_1 cos\theta_2 - sin \theta_1 sin \theta_2) \\ & y sin \theta_1 = a_1 sin ^2 \theta_2 + a_2 sin \theta_1 (sin \theta_1 cos\theta_2 - cos \theta_1 sin \theta_2) \\ & \qquad \qquad \qquad \triangledown \\ & x cos \theta_1 + y sin \theta_1 = a_1 + cos \theta_2 \qquad(1)\\ \\ \\ & x sin \theta_1 = a_1 sin \theta_1 cos \theta_1 + a_2 sin \theta_1 (cos \theta_1 cos\theta_2 - sin \theta_1 sin \theta_2) \\ & y cos \theta_1 = a_1 sin \theta_1 cos \theta_1 + a_2 cos \theta_1 (sin \theta_1 cos\theta_2 - cos \theta_1 sin \theta_2) \\ & \qquad \qquad \qquad \triangledown \\ & x sin \theta_1 - y cos \theta_1 = -a_2 sin \theta_2 \qquad(2)\\ \\ \\ & (x^2 + y^2 )cos \theta_1 = x(a_1 + a_2 cos \theta_2) +y a_2 sin \theta_2 \qquad \because x \cdot (1) - y \cdot (2) \\ & \qquad \qquad \qquad \triangledown \\ & cos \theta_1 = \frac{x(a_1 + a_2 cos \theta_2) +y a_2 sin \theta_2 }{(x^2 + y^2 )} \\ \\ \\ & (x^2 + y^2 )sin \theta_1 = y(a_1 + a_2 cos \theta_2) -x a_2 sin \theta_2 \qquad \because y \cdot (1) + x \cdot (2) \\ & \qquad \qquad \qquad \triangledown \\ & sin \theta_1 = \frac{y(a_1 + a_2 cos \theta_2) -x a_2 sin \theta_2 }{(x^2 + y^2 )} \\ \\ & \therefore \theta_1 = tan ^{-1} (\frac{y(a_1 + a_2 cos \theta_2) - x a_2 sin \theta_2}{x(a_1 + a_2 cos \theta_2) + y a_2 sin \theta_2}) \end{aligned}\]

Another way - Numerical Solution

• In contrast to the closed form(geometry solution), it absolutely needs a forward kinematics.

---

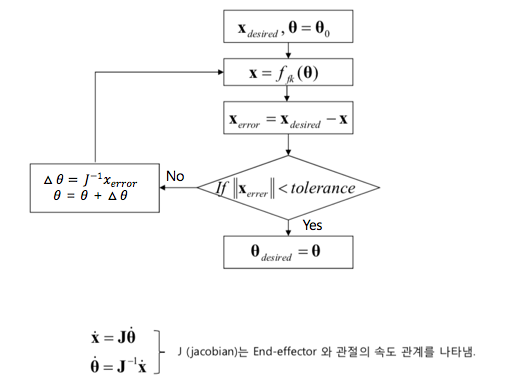
Problem 3: Velocity Kinematics

• In order to follow a contour at constant velocity, or at any prescribed velocity, we must know the relationship between the velocity of the tool(end-effector) and the joint velocities.
  • we can differentiate the equations to obtain

\[\begin{aligned} & \dot{x} = - a_1 \dot{\theta_1} sin \theta_1 - a_2 (\dot{\theta_1} + \dot{\theta_2}) sin(\theta _1 + \theta _2) \\ & \dot{y} = a_1 \dot{\theta_1} cos \theta_1 + a_2 (\dot{\theta_1} + \dot{\theta_2}) cos(\theta _1 + \theta _2) \\ \end{aligned}\]

If \(x = \begin{bmatrix} x \\ y \end{bmatrix}\) and \(\theta = \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}\), \[\begin{aligned} \dot{x} & = J \dot{\theta} \\ & = \begin{bmatrix} \frac{\partial x}{\partial \theta_1} & \frac{\partial x}{\partial \theta_2} \\ \frac{\partial y}{\partial \theta_1} & \frac{\partial y}{\partial \theta_2} \\ \end{bmatrix} \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix} \\ & = \begin{bmatrix} -a_1 sin \theta_1 - a_2 sin (\theta_1 + \theta_2) & - a_2 sin(\theta_1 + \theta_2) \\ a_1 cos\theta_1 + a_2 cos (\theta_1 + \theta_2) & a_2 cos(\theta_1 + \theta_2) \\ \end{bmatrix} \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix} \\ \end{aligned}\]

• where, J is Jacobian.

• Using inverse Jacobian give

\[\begin{aligned} \dot{\theta} &= J ^{-1} \dot{x} \\ \begin{bmatrix} \dot{\theta_1} \\ \dot{\theta_2} \end{bmatrix} &= \frac{1}{a_1 a_2 sin \theta_2} \begin{bmatrix} a_2 cos (\theta_1 + \theta_2) & a_2 sin(\theta_1 + \theta_2) \\ -a_1 cos\theta_1 - a_2 cos (\theta_1 + \theta_2) & -a_1 sin \theta_1 - a_2 sin(\theta_1 + \theta_2) \\ \end{bmatrix} \begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} \\ \end{aligned}\]

• Singular Configuration:
  • Where there is no inverse Jacobian.
  • At singular configuration, the manipulator cannot move in certain dirctions.

\[\begin{aligned} Det \quad J = a_1 a_2 sin \theta_2 = 0 \\ \therefore \theta_2 = 0 \quad or \quad \pi \end{aligned}\]

---

Problem 4: Path Planning and Trajectory Generation

Path planning

• Determines a path in task space to mode the robot to a goal position while avoiding collision with objects in its workspace, without time considerations,, that is, without considering velocities and accelerations.

Trajectory Generation:

• Determine the time history of the manipulator along a given path.

---

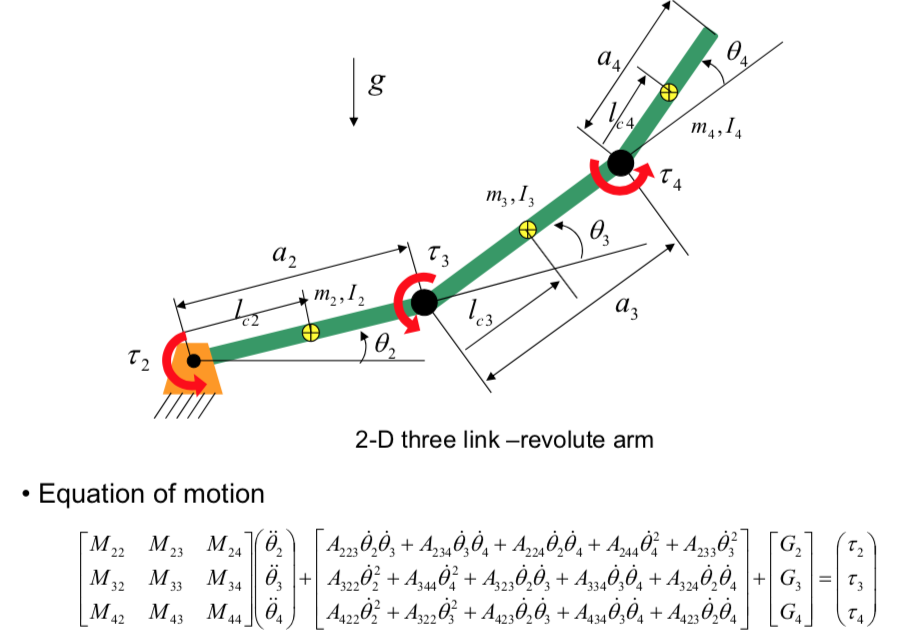
Problem 5: Dynamics

• Relationship between motion and forces(Equation of motion).
• How much force is required to achieve the given motion?
  • Rigid body dynamics: Dynamics of target object which has no strain or deformation in the body.

\[\begin{aligned} \qquad \qquad \qquad M(q) \ddot{q} + C(q, \dot{q}) \dot{q} + G(q) = \tau \end{aligned}\]

• \(M\): Inertia matrix.
• \(C\): Centrigufal and Coriolis matrix.
• \(G\): Gravity matrix.
• \(q\): Generalized coordinate(angle or position)

• \(\tau\) : Generalized force(torque or force)

• Inverse dynamics: Computes the required joint torques or forces that lead to the given robot motion.
• Forward dynamics: Computes the robot motion from the joint torques or forces applied.

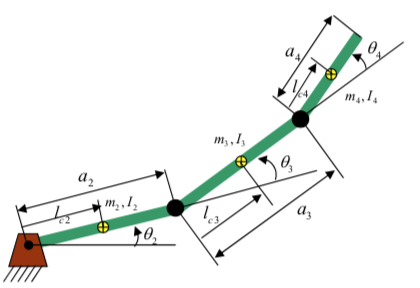
Example 1: Three link-revolute arm

---

Problem 6: Position Control

• The control prolem for robot manipulator is the problem of determining the time history of joint inputs (joint forces or torques or inputs to the actuators, for example, voltage) required to cause the end-effector to execute a desired motion.
• There are many control techniques and methodologies.
  • An important thing is that control methods depends on hardware/software and application
    • Cartesian manipulator vs. Elbow type manupulator
    • DC motor with reduction gear vs. High torgue DC motor without gwar (High tech. for interaction)
    • Point-to-point path vs. Continous path
    • More complicated hardward, the more advanced control methods.

Example: Independent Joint Position Control

• Features:
  • Simplest type of control strategy.
  • Each axis is controlled as a SISO(Single Input/Single Outpue) system.
  • Any coupling effects due to the motion of the other links is either ignored or treated as a disturbance.
  • Objectives: tracking and disturbance rejection.
    • Pose에 따라 moment가 달라져 disturbance가 달라지지만 높은 기어비 때문에 무시.

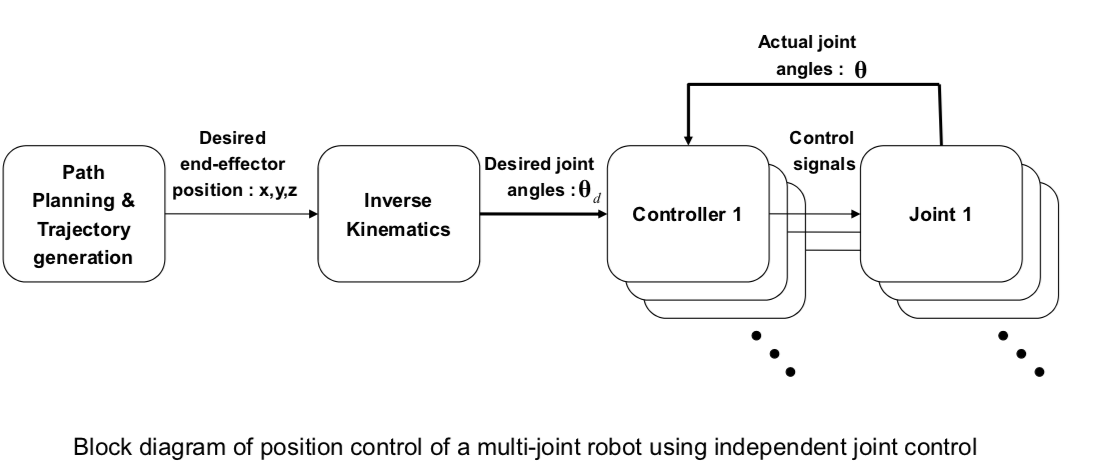
• Each joint has to follow the desired joint angle accurately!

---

Problem 7: Force Control

• Why Force Control?:
  • Pure position control is not adequate for task which involve extensive contact with the environment.
    • e.g., assembly, grinding, deburring
  • Need to control the force as well (slight deviation of the end effector would caues either to loose contact or to press too strongly).
    • We can use the Hybrid control(Position + Force control)
  • A force control strategy is one that modifies position trajectories based on the sensed forses.

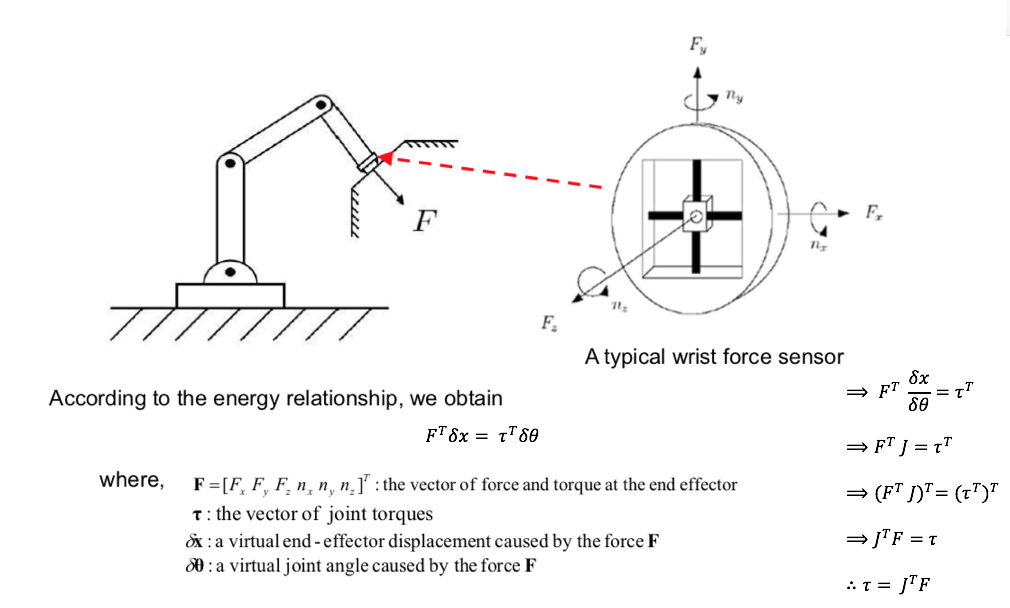
The end-effector forces are related to the joint torques!!

---

Reference:

• SEOULTECH - HRRLAB
• SEOULTECH - Robot Dynamics & Control, Lecture slides