[PAPER-Review] Learning From Demonstration

in Reinforcement learning / Reinforcement learning on Mbrl

Table of Contents

  1. [Learning From Demonstration, Stefan Schaal, 1997]
    1. Abstract
    2. Introduction
    3. Reinforcement Learning from Demonstration
      1. The Nonlinear task: Swing-up
        1. V-Learning
        2. Model-Based V-Learning
    4. The Nonlinear task: CART-POLE BALANCING
      1. Q-Learning
      2. Model-based V-Learning
    5. Pole balacing with an Actual Robot
    6. Conclusion
  2. [Exploiting Model Uncertainty Estimates for Safe Dynamic Control Learning, Jeff G. Schneider, 1997]
    1. Abstract
    2. Introduction
    3. The Algorithm
      1. Bayesian locally weighted regression
      2. Grid based Dynamics programming

[Learning From Demonstration, Stefan Schaal, 1997]

Abstract

  • 1997년도에는 사전지식 없이 처음(scratch)부터 task를 학습하는 것은 어려운 일.
    • 그러나, 사람은 드물게 처음부터 학습을 시도.
  • Control를 학습하기 위해, 이 논문은 RL의 맥락에서 demonstration으로부터 어떻게 학습을 적용되는 지를 조사
    • Demonstration들이 학습을 가속화하는 가능한 area인 task dynamics의 model, Q-function, Value-function, policy를 준비하는 것을 고려. (model, value function등을 사용하여 학습을 가속화 하겠다.)
  • 일반적인 nonlinear learning 문제에서 오직 MBRL만 demonstration이후에 상당한 속도향상을 보여주지만, LQR 문제의 경우(선형)에는 모든 method들은 demonstration으로부터 이익을 본다.
  • 이 논문에서 시연하는 복잡한 anthromorphic robot arm에서 pole balancing 구현에서는, 실제 signal processing의 복잡함에 직면할때 MBRL은 LQR 문제에 대해 가장 큰 robustness 를 제공.

Introduction

  • \(1.\) Inductive supervised learning 방법은 정교함의 높은 수준에 도달.
    • Nature에 대한 사전 지식들이나 data set이 주어지면, error criterion를 최소화하여 data로부터 structure를 추출하는 알고리즘의 host가 존재.
  • 그러나, Control를 학습하는 방법에서는 task를 학습하는 것은 잘 정의되지 않음
    • 여기서, 목표는 policy를 학습하는 것.
    • i.e., task를 성취하기 위한 dynamical system으로 유도하는 거나 인지한 state에 반응하여 적절한 행동을 하는 것.
    • Task는 일반적으로 임의의 performance index의 관점에서 묘사되기 때문에, 지도하는 방법으로 controller를 학습하는 data를 직접적 학습하는 것은 존재하지 않음
      • 더욱 문제가 되는 것은, performance index는 task의 long term 행동에 걸쳐 정의 가 되며 현재 performance에 대해 과거의 행동이 얼마나 좋은지(credit) 안좋은지(blame)를 결정하는 temporal credit assignment 문제가 발생.
      • 위와같은 setting(RL에 대해서는 일반적)에서, 처음부터 task를 학습하는 것은 good policy를 찾기 위해서 state-action space의 exploration의 time-consuming amount(소요시간)을 상당하게 요구.
  • \(2.\) 반대로 사전 지식 없이 학습하는 것은 인간이나 동물이 거의 취하는 않는 접근
    • New task에 접근하는 방법에 대한 knowledge는 이전에 학습된 task에서 transfer 가능 ang/or teacher의 performance로 추출.
    • New task를 빠르게 성취하기 위해 다양한 정보로 control을 하는 것은 아직 open questions.
    • 이 논문: Demonstration에서 학습을 focus 할 것
  • \(3.\) Demonstration에서 학습하는 것: “programming by demonstration”, “imitation learning” teaching by showing”으로 알려짐.
    • 목표: 전문가에 의해 assembly task를 로봇하게 단독으로 보여주는 automatic programming process을 시간이 많이 소요되는 로봇의 manual programming을 대체하고자 함.
    • 이 논문: RL과 demonstration으로부터 learning이 어떻게 이익이 되는지에 집중
    • RL을 2개 카테고리로 분류
      • Section2) Nonlinear task에 대한 RL
      • Section3) (Approximately) linear task에 대한 RL
    • Q-learning, value-function learning, model-based RL와 같은 method는 demonstration으로부터 data에서 이익을 볼 수 있는 방법을 조사.
      • Section 2.3, example task, pole balancing은 이를 학습하기 위해 실제 anthropomorphic을 사용.
      • 더욱 복잡한 상황에서 demonstration으로부터 학습의 적용가능성 재고려.

Reinforcement Learning from Demonstration

  • 두 개의 task는 demonstration에서의 학습을 살펴보는 basis.
    • Nonlinear task: pendulem swing-up with limited torque
    • (Approximately) Linear task: cart-pole
    • 두 task에서, learner는 one-step reward \(r\)이 주어지고, continuous state 및 action 문제로 formulation.
    • 각각의 목표는 infinite horizon discounted reward를 최소화하는 policy를 찾는 것

여기서, 왼쪽 eqn: continous time formulation, 오른쪽 eqn: discrete time version. x: n-차원 state vector, u: m차원 입력 vector. \[\begin{aligned} V(x(t)) = \int^{\infty}_t e^{-\frac{(s-t)}{\tau}} r(x(s),u(s)) ds \quad or \quad V(x(t)) = \sum^{\infty}_{i=t} \gamma ^{i-t} r(x(i), u(i)) \end{aligned}\]

  • Swing-Up에 대해, teacher는 다른 initial condition에서 시작한 5 개의 성공적 시도를 제공한다고 가정.
    • 각각의 시도는 60Hz로 샘플링되는 data vector \((\theta, \dot{\theta}, \tau)\)의 time series로 구성
  • Cart-Pole에 대해, 성공적인 balancing의 30초 demonstration을 가지며, data vector \((x, \dot{x}, \theta, \dot{\theta}, F)\)

어떻게 RL을 가속화하기 위해 demonstration이 사용되는 방법은?

The Nonlinear task: Swing-up

  • Swing-up에 task에 대해서 Value fucntion(V-function) (Dyer & McReynolds, 1970)을 학습하는 기반으로 하는 RL을 적용하고, 대안적인 방법으로 Q-learning(Watkins, 1989)은 continous state-action space에 대해 아직 limited research를 받음.
    • V-function은 scalar reward value \(V(x(t))\) 각 state에 대해 assign하고 다음 consistency equation을 만족:
\[\begin{aligned} V(x(t)) = argmin_{u(t)} (r(x(t), u(t)) + \gamma V(x(t+1))) \qquad(2) \end{aligned}\]
  • 이 방정식은 discrete state-action system; continuous formulation은 (Doya(1996))참조
    • Optimal policy: \(u = \pi(x)\), (2)를 만족하는 state x에서 action u를 선택.
    • 이 계산은 subsequent state x(t+1)의 knowledge를 포함하는 optimization step를 포함.
      • 따라서, controlled system 의 dynamics의 model(\(x(t+1) = f(x(t), u(t))\)) 이 필요.
    • Demonstration에서의 학습하는 관점에서는, V-function 학습은 demonstration에서 준비(가공, primed)될 수 있는 3가지 후보를 제공.
      • Value function \(V(x)\)
      • Policy \(\pi(x)\)
      • Model \(f(x,u)\)
V-Learning
  • Swing-Up에 대해 demonstration의 benefit을 평가하기 위해서, Doya’s(1996) 에서 제안된 continous TD(CDT) 학습으로 V-learning을 구현.
    • V-function 및 dynamics model은 nonlinear function approximator(Receptive Field Weighted Regression-RFWR))에 의해 점차적으로 학습됨.
      • NN의 발전이 크지않아 approximator를 다른 방법으로 사용한 것 같음
    • Doya’s 방법과 다른 것은 policy \(\pi\) (“actor” as in Barto Barto et al. (1983))의 model를 학습하기 위해 CTD에서 제안된 optimal action을 사용 (RFWR으로 표현됨).
  • 다음의 학습 condition들은 경험적으로 실험:
    • a) Scratch : 처음부터 value function V, model f, actor \(\pi\) 의 trial by trial learning.
    • b) Primed Actor : demonstration에서의 \(\pi\)의 초기 training 이후, trial by trial learning.
    • c) Primed Model: demonstration에서 f 의 초기 training 이후, trial by trial learning.
    • d) Primed Actor & Model : b) 및 c)에서의 \(\pi\) 와 f 의 priming 이후, trial by trial learning.
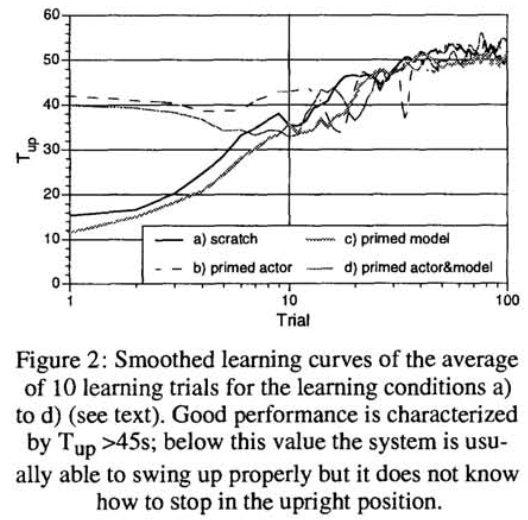
An image with a caption
  • Fig. 2는 Swing-up 학습 결과
    • 각 trial은 60초 지속
    • Time \(T_{up}\)은 각 trial 동안 \(\theta \in [-\pi/2, \pi/2]\) 에서 pole이 보내는 시간.
  • a) 와 c)를 비교: Demonstration에서의 pole model 학습은 가속화되지 않음.
    • 당연한 결과: V-function을 학습하는 것은 model을 학습하는 것보다 상당히 복잡하고, 이것은 학습 과정은 V-function learning에 의해 우선시(dominate)된다.
    • 흥미롭게도, demonstration에서 action를 priming은 초기 performance(condition a vs. b)에서 상당한 효과를 가진다.
  • 시스템은 pendulum을 pump up 시키는 올바른 방법을 알고 있지만 upright position에서 pendulum을 balancing하기 위해서는, 결국 처음부터 학습하는 것처럼 동일한 시간이 소요.
    • 이 행동은 이론적으로 V-function이 전체 state-action space가 densely explore 되어지면 유일하게 정확하게 근사 되어질 수 있기 때문.
    • 전체 state-action space에 대한 정보를 알아야 최적의 해를 구할 수 있음
    • 만약 demonstration이 전체 state space의 많은 부분을 cover하는 경우에는, V-learning은 이익을 볼 수 있을것이라 예상.
  • V-function만을 prime거나 다른 함수들을 가지고 조합하는 demonstration을 사용하는 것도 조사.
    • 이 결과들은 정량적으로 Fig. 2와 동일:
      • 만약 policy가 priming에 포함되어 있다면, learning traces는 b), d)와 같고 다른 경우는 a), c)
    • 다시말하지만, 이것은 전체적으로 놀라운 결과는 아니다.
      • V-function을 근사시키는 것은 단순히 \(\pi, f\)에 관한 supervised learning이 아닌, (2)(consistency equation)의 validity(타당성)를 확인하기 위한 iterative 절차를 요구하고 복잡한 nonstationary funtion approximation 과정에 해당.
      • Demonstration으로부터 data가 제한되면, 일반적으로 좋은 value function을 근사는 불가능.
Model-Based V-Learning
  • model f 를 학습하는 것은, 이를 더욱 강력하게 사용가능.
    • certainty equivalence의 원리에 따르면, f 는 real world를 대체할 수 있고 real world와 interaction대신에 “mental simulations”에서 planning이 동작될 수 있음.
    • RL에서, 이 idea는 원래 discrete state-action space에 대한 Sutton’s(1990) DYNA 알고리즘에 의해 제안.
    • 여기서 DYNA, DYNA-CTD의 continuous 버전이 얼마나 learning from demonstration에서 도움이 될 수 있는지를 탐구(explore)할 것.
    • Section 2.1.1(V-Learning)에서 CTD와 비교하여 얻은 유일한 차이점은 모든 real trial 이후에, DYNA-CTD는 지금까지 획득한 dynamics 모델이 실제 pole dynamics를 대체하는 다섯 번의 “mental trials”을 수행.
    • 두 개의 learning conditions:
      • Scratch: 처음부터 V, model f, policy \(\pi\)의 trial by trial learning.
      • Primed Model: demonstraion으로부터 f 의 초기 training 이후, trial by trial learning.
    • Fig. 3.는 이전 section에서 V-learning과 대조적.
      • Learning from demonstraion은 상당한 차이를 보임
        • Stable balancing을 가지는 좋은 swing-up을 성취하기 위해서는 단지 demonstration 이후 2-3 trial만 필요, \(T_{up}\) > 45s.
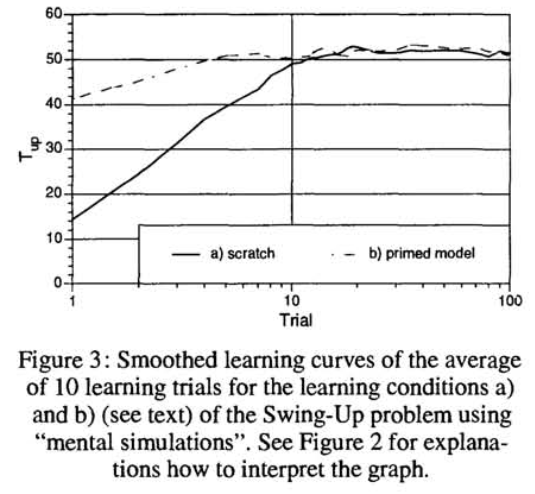
An image with a caption

Note that

처음부터 학습하는 것도 Fig. 2.보다 상당히 빠름.

The Nonlinear task: CART-POLE BALANCING

  • Swing-Up task에 대한 demonstration으로부터 RL를 적용하는 것은 시기상조.
    • Nonlinear function approximation을 가진 RL은 아직 적절한게 없음(yet to obtain appropriate scientific understanding).
    • 따라서, 이 section에서 좀 더 쉬운 task(cart-pole balancer)로 변경.
    • 이 task는 pole이 upright position에 가까울 때, approximately linear.
    • 이 문제는 LQR(Dyer & McReynolds, 1970)의 맥락에서 DP literature에서 잘 연구됨.

Q-Learning

  • V-learning과 대조적으로, Q-learning(Watkins, 1989; Singh & Sutton, 1996)은 value function보다 더욱 복잡, Q(x, u), state 및 command(input)에 의존.
  • consistency equation (2)와 유사한 Q-learning:
\[\begin{aligned} Q(x(t), u(t)) = r(x(t), u(t)) + \gamma argmin_{u(t+1)} (Q(x(t+1), u(t+1)) \qquad(3) \end{aligned}\]
  • 매 state x 마다, reward function (1)하에서 optimal action이고 Q를 최소화하는 action u 를 선택.
    • 장점: optimal policy를 찾기 위해 Q-function을 평가하는 것은 제어할 대상의 dynamical system f 를 요구하지 않음;
      • 오직 one-step reward r 의 값만 필요
    • Demonstration에서 learning하기 위해서는, Q-function and/or policy를 priming하는 것은 learning을 가속화하는 두 개의 후보이다.
  • LQR 문제는 Bradtke (1993)가 policy를 추출한 것을 기반으로하는 demonstration에서 이상적으로 학습에 적합한 Q-learning 방법을 제안.
    • LQR에 대해 Q-function이 state 및 commands(input)이 quadratic인 것을 관측.
    • Gain matrix K 로 표현되는 (linear) policy는 (4) 에서 (5) 와 같은 추출 할 수 있다.
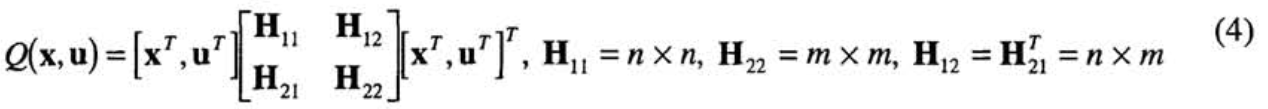
An image with a caption
\[\begin{aligned} u_{opt} = -K x = - H ^{-1} _{22} H _{21} x (5) \end{aligned}\]

  • 반대로, stabilizing initial policy \(K_{demo}\) 가 주어지면, 현재 Q-function은 recursive least squares procedure에 의해 근사 되고 수렴성이 보장되는 (Bradkte, 1993) policy iteration 과정에 의해 최적화.

  • corresponding obseved states x 에 대한 observed command u 를 linearly regressing함으로서 초기 policy \(K_{demo}\) 를 추출 하도록 demonstration이 허용하기에, pole balancing의 one-shot learning을 성취하는 것.

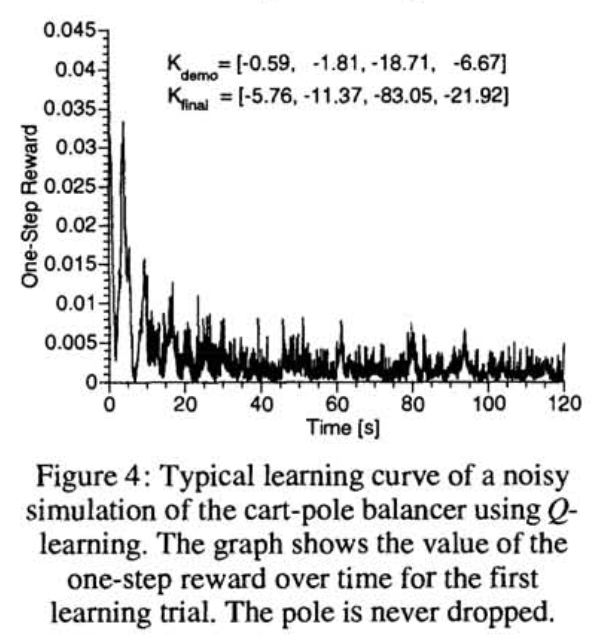
An image with a caption
  • Fig. 4.를 보면, 120초 정도 후(12 policy iteration step)에, policy는 기본적으로 optimal policy와 기본적으로 구별 불가
    • 그러나, Q-learning의 주의사항은 stabilizing initial policy없이 학습불가

Model-based V-Learning

  • V-function을 학습 하여 LQR task를 학습 하는 것: DP(Dyer&)의 classic form 중의 하나.
    • Stabilizing initial policy \(K_{demo}\) 를 사용하여, 현재 V-function 은 Bradtke (1993)과 유사하게 recursive least square에 의해 근사.
    • \(K_{demo}\) 와 유사하게, cart-pole dynamics의 (linear) model \(f_{demo}\) 은 cart-pole state x(t)의 linear regression에 의해 demonstration에서 추출 vs. 이전 state 및 command vector (x(t-1), u(t-1)), model은 학습 중에 경험하는 매번 새로운 data point을 가지고 정제될 수 있음.
    • Policy update:
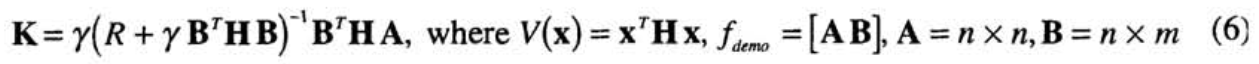
An image with a caption
  • 따라서, Bradtke(1993)와 같이 유사한 과정은 optimal policy K를 찾기 위해 사용될 수 있고, system은 one shot learning을 성취하며, Fig. 4와같이 정량적으로 구별 불가.

V-learning, Q-learning과 다르게 model이 필요, \(f_demo\) = [A B]

  • Section 2.1.2 (이전 Model-Based V-Learning)에서 지적했던 것처럼, mental simulation을 수행함으로써 학습된 모델을 더욱 효율적으로 사용하도록 만듬.
    • model \(f_{demo}\)이 주어지면, policy K은 H의 초기 추정치로부터 off-line policy iteration에의해 계산 할 수 있고, e.g., identity matrix (Dyer & McReynolds, 1970)로 취해짐.
    • 따라서, initial (stabilizing) policy가 요구되지않고, task dynamics의 추정치를 요구.
    • 또한, 이 방법은 one shot learning을 성취.

Pole balacing with an Actual Robot

  • 이전 section의 결과로서, LQR 문제들에 대해 model-based V-learning 및 V-learning, Q-learning간의 실제 성능 차이는 없는 것 같음
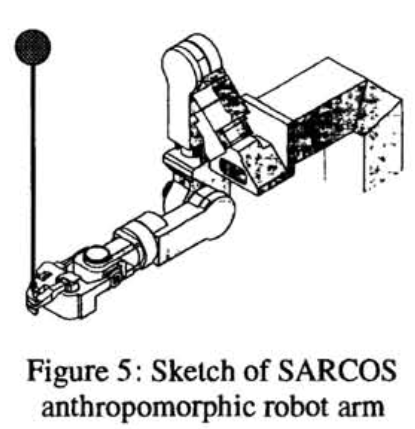
    • 더욱 realistic framework에서 이러한 방법들의 유용성을 검증하기 위해서, anthropomorphic robot arm에서 pole balancing의 demonstration에서의 learning을 구현
      • Robot은 60Hz video-based stereo vision 장착.
      • Pole은 real-time으로 track할 수 있도록 두 color blob들로 표기.
      • 두개의 전면 카메라를 세우고 human에 의해 pole balancing의 30초 long demonstration이 제공.
  • Simulation과 비교하여 몇가지 중요한 차이점:
    1. demonstration이 vision-based이므로, kinematic 변수들만 demonstration에서 추출할 수 있다.
    2. visual signal processing은 120ms의 시간지연을 가진다.
    3. robot에 주어진 command는 로봇의 unknown nonlinearities때문에 높은 정확도를 가지는 execution은 아니다.
    4. human은 pole balancing에 대해 internal state를 사용한다
      • 즉, human policy는 부분적으로 non-observable variables을 부분적으로 기반한다.
An image with a caption
  • 위와 같은 issue들은 다음과 같은 영향을 가진다:
  • Kinematic Variable:
    • 구현은 robot arm은 Cart-Pole problem의 cart로 대체.
    • Arm의 inverse dynamics, inverse kinematics의 추정치를 가지므로, Cartesian 공간에서 task에 command input으로 finger의 가속도 사용 가능.
    • Arm은 또한 pole보다 훨씬 무거워, pole이 arm에 발휘하는 interaction force를 무시함.
    • 따라서, Fig. 1b의 pole balancing dynamics는 (7) 와 같이 reformulation
      • Equation에서 모든 변수들은 demonstration에서 추출 가능.
      • 이러한 방정식의 extension은 생략.
\[\begin{aligned} uml cos \theta + \ddot{\theta} m l^2 - mgl sin \theta, \ddot{x} u \quad (7) \end{aligned}\]
  • Delayed Visual Information:
    • Delayed vaeiables를 다루는 두 가지 방법:
      • \(1\). Sytem의 state에 7*1/60s = 120 delay time, \(x^T = (x, \dot{x}, \theta, \dot{\theta}, u_{t-1}, u_{t-2}, ..., u_{t-7}\), 와 일치하는 delayed commands을 augmentation
      • \(2\). state predictive controller를 employ하는 방법.
      • 첫 번째 방법은 policy의 complexity를 상당히 증가, 두번째 방법은 model _f_를 요구.
  • Inaccuracies of Command Execution:
    • 가속도 명령 u 가 주어지면, 로봇은 u 에 가깝게 실행하지만 정확한 u 는 아님.
    • 따라서, u 를 포함한 function을 학습하는 것(e.g., dynamics model)은 위험할 수 있으며, 이유는 mapping \((x, \dot{x}, \theta, \dot{\theta}, u) \rightarrow (\ddot{x}, \ddot{\theta})\) 이 robot arm의 nonlinear dynamics에 의해 contaminated(오염)되기 때문이다.
    • 게다가, 이러한 model을 믿을만하게(reliably) 학습할 수 없다고 밝혀졌다.
    • 이것은 command u 를 “관측(observing)”하여 개선(remedied)될 수 있다
      • 즉, visual feedback으로부터 \(u = \ddot{x}\)을 추출.
  • Internal State:
    • Human은 pole balancing에서 internal state 사용.
    • 따라서, policy는 Section 2.2(THE LINEAR TASK: CART-POLE BALANCING)에서 주장했듯이 더욱 쉽게 관측될 수 없다
      • Teacher의 policy를 추출하기 위한 regression analysis는 현재 state 및 과거 command(s)의 적절한 time-alignment를 찾아야만 한다.
      • Delayed commands에 기반한 policy를 regressing이 singular regression 행렬들에 의해 위험(endanger)해지게되면, 수치적으로 관련된 과정이 될 수 있다.
    • 결과적으로, Section 2.2에서 설명했듯이 Q-learning, V-learning의 응용을 막아버리는, demonstration에서 nonstabilizing policy를 추출하는 것은 쉽게 일어 난다.
      • policy를 추출할때 방해요소는 쉽게 발생

    • 이러한 고려사항의 결과는, demonstration에서 추출하기 하는 가장 믿을만한 요소는 pole dynamics의 model .

    • 저자의 구현에서는, (6, Model-based V-learnign)와 같이 policy를 계산하기 위해서 사용되는 두가지 방법이 있고, visual information processing에서 delay를 극복하기 위해 Kalman filter를 가지고 state-predictive control을 사용.
      • model은 RFWR(Schaal & Atkeson 1996)의 구현으로 real-time으로 점진적으로 학습
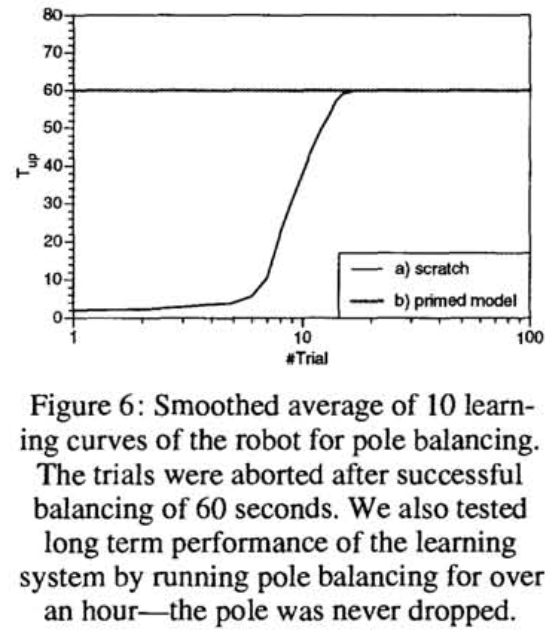
    • Fig. 6은 실제 로봇의 demonstration에서의 학습과 처음부터 학습의 결과를 보여줌.
      • Demonstration이 없다면, 1분이상 지속하는 학습은 10-20 trial이 소요.
      • 30초 long demonstarion을 가지면, 학습은 one single trial로 믿을만하게 성취
        • 다양한 사람의 demonstration들을 사용하고 다양한 pole을 사용.
An image with a caption

Conclusion

  • Q-learning, V-learning, model vased RL에 초점을 맞춘, RL 맥락에서 learning from demonstration을 다뤘다.
  • World의 predictive model을 추출, Q/Value function을 prime하여 demonstration data를 사용, policy를 추출하여 demonstraion에서 Q-learning 및 value function learning은 이론적으로 이득을 봄.
    • 그러나, LQR 문제의 special case에서만 demonstration으로부터 learner를 priming하는 상당한 이익을 찾음.
    • 대조적으로, model-based RL은 “mental simulations”에 대해 world의 predictive model을 사용하여 demonstration으로부터 많은 이득을 취할 수 있었다.
  • Anthropomorphic robot arm 구현에서, LQR 문제에서 구현
    • MBRL은 Q-learning, value fucntion learning보다 실제 learning 시스템에서 complexity에 대해 더욱이 robust함을 제공
    • Model based 방법을 사용하여 single trial에서 demonstration에서 로봇이 pole-balancing을 매우 좋은 reliability을 가지고 학습
  • 이 논문에서 가장 중요한 것은 모든 학습 접근방법이 동등하게 knowledge를 transfer and/or biases의 결합이 동등하게 적용되지 않는다는 것

[Exploiting Model Uncertainty Estimates for Safe Dynamic Control Learning, Jeff G. Schneider, 1997]

Abstract

  • DP와 결합한 model learning 은 continuous state dynamic system의 control을 학습하는데 효과적.
    • 가장 단순한 방법은 학습된 model이 정확하다 가정하고 DP에 적용, 그러나 많은 approximator들은 fitting하는데에 불확실한 추정치를 제공.
    • 어떻게 exploit될까?
      • 이 논문은 system이 학습하는 동안 재앙과 같은 실패를 가지는 것을 막기 위한 case에 대해 다룸.
      • 저자는 dual control literature를 개조(adapt)하여 새로운 알고리즘을 제안하고 DP를 가지고 Bayesian locally weighted regression model을 사용
  • 일반적인 RL 가정은 공격적인(aggressive) 탐험(exploration)이 되기를 장려한다.
    • 이 논문은 system이 exploration 해야하는 것의 반대(converse) 경우를 다룸
    • 알고리즘은 4차원 simulated 제어 문제에서 구현.

Introduction

  • RL 및 관련 grid-based DP 기술은 지속적으로 continuous 값을 가지는 state space를 가지는 dynamic system에 점차 적용 이 되고 있음(1997 년도).
    • 1997 년도까지의 연구 결과:
      • [Gordon, 1995] Value(or cost-to-go) 함수를 표현하기 위해 다양한 interpolation을 사용하여 continuous 값을 가지는 state spaces에 RL을 적용하여 완전한(sound) 이론적 근거를 가지는 DP 방법의 수렴성 증명.
        • 이러한 방법(continous 문제의 수렴성 증명)들은 산업 학습 및 제어 문제에 응용을 향하기 위한 중요한 과정.
      • [Sutton, 1990, Moore and Atkeson, 1993, Schaal and Atkeson, 1993, Davies, 1996] system을 구동한 data가 model을 build하기 위해 사용할 때, data 및 계산적 효율성에서 상단한 이익이 있다는 것이 보고됨.
        • (Q-learning이 하는 것과 같이) 단일 value function update를 위해 한번 진행하고 버리는 방법 = 비효율적.
        • DP sweeps은 off-line 혹은 on-line으로 학습된 모델에서 수행될 수 있다.
      • Vanilla 형식에서, 이 방법은 model이 정학하다 가정하고 model을 사용하여 deterministric DP를 수행.
        • 이 가정이 종종 정확하지 않음, 특히 학습의 초반 구간.
        • 시뮬레이션 혹은 software 시스템을 학습할 때, 이 가정이 성립하지 않는다는 사실(model 정확)은 아무런 해가 없을 수도 있으나, 실제에서 physical 시스템은 실제로 catastrophic state이고 학습하는 동안에는 이를 피해야만 함.
        • 더 나쁜 것은, 학습이 시스템의 정상 동작중에 발생해야만 하면 이는 학습 동안의 성능이 상당히 저하되지 않아야 한다.
  • Adaptive, optimal linear control이론 자료는 이 문제는 상당히 stochastic, dual control이라는 이름으로 살펴보고 있다.
    • [Kendrick, 1981, Bar-Shalon and Tse, 1976] 에서 살펴볼 수 있음.
    • 제어 의사 결정(control decision)은 deterministic, cautionary, probing 용어 들에 기반
      • Deterministic term: 모델이 완벽하고 best performance에 대해 control한다 가정
        • 모델이 부정확하면 망함
      • Cautionary term: model에 uncertainty를 고려하는 controller를 생성하고 최적이라 기대하는 성능(best expected performance)에 대해 control 선택.
        • 시스템이 동작중에 system이 학습한다면, model에 대한 좋은 data를 얻기 위해 suboptimal and/or risky인 control들을 선택하는 것이 현명할 수도 있으며 궁극적으로 더 좋은 long-term 성능을 얻을 수 있음.
      • Probing(exploration) term: best long-term 성능을 생성하는 controller를 제공.
  • Dual Control의 장점: strong 수학적 기반으로 system, model, noise, performance criterion에 대한 몇 가지 가정하에서 optimal learning controller를 제공.
    • RL와 같은 DP 방법 은 system이나 performance measure의 형태에 대한 강한(strong) 가정들을 만들지 않는 장점.
    • [Atkeson, 1995, Atkeson, 1993]: caution, probing 이 포함된 global linear control을 사용한 기술을 제안했으며, local case에서도 응용 가능.
    • 저자의 논문은 Bayesian locally weighted regrtession model의 사용을 통해 dual control으로부터 cautionary 개념을 가지고 grid based dynamic programming을 결한한 알고리즘 제안
  • 저자의 알고리즘은 산업 제어 응용을 염두에 두고 설계
    • 전형적인 시나리오는 생산 라인이 지속적으로 동작된다는 것.
    • 이러한 동작에서 이용가능한 data가 있지만, state space의 작은 영역만을 다룰 수 있기에 전체 동작하는 potential range에 걸쳐 정확한 모델을 생성하기 위해 사용되어 질 수 없음.
    • Management는 set point 혹은 외란(disturbance)의 변화에 반응하는 line의 성능향상에 관심있지만, learning process 중에는 생산손실(loss of production)이 크면 안된다.

The Algorithm

  • Dynamics \(x^{k+1} = f(x^k, u^k)\)로 구어진 system을 고려.
    • state x, contron u, : real valued vectors.
    • k : discrete time increments.
    • f 의 model: \(\hat{f}\).
    • Task는 form \(J = \sum^N _{k=0} L(x^k, u^k, k)\) subject to the system dynamics 의 cost functional 최소화.
      • N: 문제에 따라 fixed 일수 있고 아닐 수도 있음.
      • L은 주어지고, f은 학습해야함.
      • 목표: 학습 도중에 큰 손해 발생(incurring huge penalties)없이 J 를 최소화하기 위해 f 를 학습하기 위해 data를 얻는 것.
    • Cost function이 catastrophic states를 정의한다는 implicit 가정 존재.
      • 만약 피해야하는 disaster가 없다면, 단순하고 더욱 aggressive 알고리즘이 저자가 제안한 알고리즘보다 성능이 좋을 것.
  • Top level 알고리즘:
    1. 기존 controller로부터 system을 구동하는 도중에 data 획득.
    2. Baysian locally weighted regression 사용하여 data로부터 model 구축
    3. Value function, policy를 계산하기위해 model를 가지고 DP 수행
    4. 새로운 policy를 사용하여 system 구동하고 추가 data 확보.
    5. 성능 향상하는 동안 step 2 반복

Steps 2, 3 설명은 나머지 section에서 진행.

Bayesian locally weighted regression

  • 저자는 data로부터 model을 build하기 위해서 Baysesian locally weighted regression[Moore and Schneider, 1995]이라 불리는 locally weighted regression [Cleveland and Delvin, 1988, Atkeson, 1989, Moore, 1992] 의 형태를 사용.
  • Query, \(x_q\)가 만들어 질 때, 저장된 data points의 각각은 weight \(w_i = exp( - \left \| x_i - x_q \right \| ^2 /K)\) 을 수신
    • K : regression에서 localness의 양을 제어하는 kernel width
  • Bayesian LWE에 대해 저자는 regression model의 계수 및 noise covariance에 대해 wide, weak normal gamma를 먼저 가정.

  • prediciton의 결과는 output에 대한 distribution이고, output은 data의 없어도 잘 정의됨 (see [Moore and Schneider, 1995] and [DeGroot, 1970] for details)

  • Data가 없는 regions에서의 prediction의 distribution은 DP 알고리즘의 performance에 중요.
    • Search 및 실험(experimentation)을 통해학습하는 경우가 많기 때문에, 얼마나 data가 많은 region에서 interpolate하는 것만큼이나 data가 없을 때 무지(own ignorance)를 fucntion approximator가 예상하는 것도 중요.

Grid based Dynamics programming

© 2020. All rights reserved.

Powered by Hydejack v8.1.1