Digital Motion Control System: Lecture1- Motion Profile
in Robotics / Robotics & Control on Digital_motion_control
Table of Contents
구동 프로파일
- 제어 목표치가 고정되어 있는 경우: 레귤레이팅(regulating) 제어
- 제어 목표치가 시간에 대하여 변화하는 경우: 추종(tracking) 제어
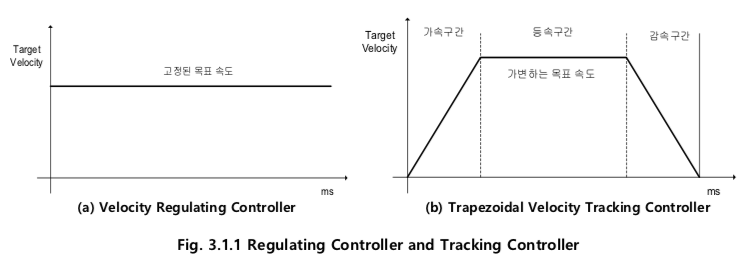
- Fig. 3.1.1(a)와 같은 레귤레이팅 제어기는 구조가 비교적 단순, 피드백 제어기가 주축.
트래킹 제어기의 경우에는 제어 목표값 이 Fig. 3.1.1(b)와 같이 시간에 대해 변화 하므로, 제어 목표값에 대한 변화 경로를 사전에 설계 해주어야 하고, 제어 성능의 향상을 위하여 피드포워드(feedforward) 제어기를 피드백제어기와 병행해서 사용.
- 특정점 A에서 B로 움직일 때 우선적으로 정해야 하는 것은,
- 주어진 거리를 얼마만한 시간에 도달해야 하는가 하는 문제
- 시간에 따른 움직임의 위치, 속도 등의 목표 궤적을 설계.
- 목표 위치 궤적의 2차 도함수(목표 가속도 선도)가 바로 모터에서 발생해야 하는 힘의 궤적 과 형상이 동일.
구동 프로파일과 구동시간.
- 관성을 가진 물체는 급격한 속도 변화를 발생시키기가 매우어려움.
- 우선 사다리꼴 속도 프로파일의 위치에 대한 목표값과 가속도 목표값을 도시.
- 모터를 제어할 때 위치 목표값과 가속도 목표값은 각각 속도 목표치를 적분한 값, 미분한 값의 관계
- 셋 중에 하나의 프로파일만 정해지면 나머지는 수학적인 관계에 의해 자동으로 구해짐.
- 주로 처음 시작 구간의 위치프로파일 함수의 차수를 지칭 (Fig.3.2.1과 같은 경우 ‘2차 구동프로파일’)
- 부드러운 다항식(polynomial)의 형상을 기본으로 차수를 높여가면서 설계하는 방법도 존재
- 사다리꼴 형태를 기본으로 하는 구동 프로파일은 실제 DSP에 내장될 때 수식의 형태 로 내장하는 것이 편리한 반면, 부드러운 다항식의 형상과 구속조건을 사용하여 설계하는 방법은 테이블 방식 으로 저장되어 사용하는 경우 매우 편리.
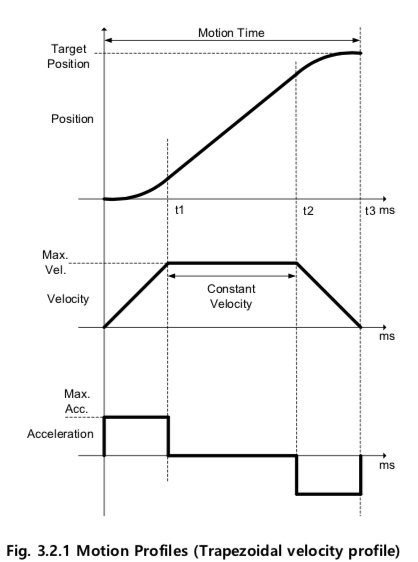
- 등속 구간에 집입하는 시점: \(t_1\), 등속 구간이 끝나는 시점: \(t_2\), 원하는 목표점에 도달하는 시간(가속,등속, 감속의 전체 구동에 필요한 총 시간): \(t_3\)
- 이러한 구동 프로파일은 제어기의 인터럽트 제어시간마다 목표치가 생성되어야 하므로, 구동이 시작되기 이전에 \(t_1, t_2, t_3\)를 구동거리 및 최대속도, 최대가속도에 따라 어떻게 정해서 운용할 것인지 구동전에 미리설계.
- 많은 경우 그 시스템이 허용하는 가장 짧은 최소 구동 시간 으로 구동해야 하는 경우가 발생.
- 생산성 UPH(Unit Per Hour, 단위시간 생산량)의 향상과 직결. But, 하드웨어 및 구동능력이 달라서 최소구동시간이 다를텐데 어떠한 방법으로 계산하고 설계?
- 구동거리가 매우 짧은 경우: 최대속도에 도달하기 전에 이미 감속이 되어야 함(Fig. 3.2), 등속 구간이 형성 안됨.
최소구동시간에 영향을 주는 요소
- 특정 스테이지에서 정해진 거리에 대한 최소 구동시간은 몇 가지 시스템의 한계에 의해 결정
- 최대허용속도
- 최대허용가속도
- 최대허용저크
최대허용속도
- 서보 시스템 구동의 최대 허용 속도는 아래 요소에 의해 주로 결정:
- 모터 자체의 최대 회전 속도
- 위치 피드백 센서인 엔코더의 최대 출력 주파수
- 엔코더 값이 입력되는 카운터 부의 최대 입력 주파수
- 여기서 한가지 더 고려해야 할 것은
- 모터의 회전에 따른 역기전력이 모터 드라이버의 버스 전압보다 작아야한다는 것(여기서 고려하지는 않음)
- 모터 자체의 최대 회전 속도가 충분히 높을 때는 엔코더 시스템 을 보다 자세히 들여다 보면,
- 정현파를 출력하는 엔코더 헤드부
- 정현파를 잘게 쪼개어 미세한 해상도를 얻어내는 엔코더 채배기
- 디지털 펄스로 출력되는 위치 신호를 저장하는 카운터
- 다음의 3 가지 요소는 서보 시스템에 위치 피드백 센서 에서 최대허용속도에 영향을 주는 요소
- 정현파를 생성하는 엔코더의 헤드부 제한 속도 :
- 엔코더의 헤드부에서 내부적으로 출력되는 정현파는 광 다이오드로 구성되어 속도가 빨라짐에 따라 그 신호의 크기가 줄어들기 때문에, 저주파에서의 신호 크기를 기준으로 -3dB(선형 스케일로 신호의 크기가 70.7% 되는 상태) 되는 주파수를 일반적으로 최대출력주파수 로 규정
- 엔코더 채배기의 입력 주파수의 한계 :
- 엔코더 채배기는 정현파의 Sin, Cos 신호를 잘게 나누어 해상도를 높여주는 역할 을 하는데, 보통 20, 32, 50, 64, 128, 256, 1024 채배 등을 많이 이용한다. 이 채배기 또한 내부에 AD 컨버터converter, 고주파 클럭clock 그리고 광대역 OP 앰프 등으로 구성되어 있으므로 최대 허용 입력 주파수가 따로 존재. 채배값을 바꾸어서 사용하는 경우, 최대출력주파수 또한 고려되어야 한다.
- 카운터의 입력 주파수의 한계:
- 일반적으로 DSP 보드나 제어기 보드의 경우, 카운터는 FPGA(Field Programmable Gate Array), EPLD(Erasable Programmable Logic Device)등으로 설계하는 것이 보편적인데, 보통 카운터 쪽의 입력부에 4채배 로직을 설계하여 이전 단의 채배기에서 나온 A상, B상의 펄스 신호를 마지막으로 4채배를 더 해주는 것이 현재의 서보기술에서는 일반적인 형태. 따라서 이러한 카운터에 기본으로 내장된 4채배 로직이 정상적으로 작동하기 위해서는 반드시 EPLD의 동작 클럭 주파수가, 구동부가 최대 속도로 움직일 때의 채배기 출력 펄스 주파수의 4배 이상 이 되어야 함.
- 정현파를 생성하는 엔코더의 헤드부 제한 속도 :
최대허용가속도
최대허용가속도는 마찰력을 무시하면 모터가 발휘할 수 있는 최대힘 및 부하의 크기 에 의해서 결정되므로, 결과적으로 부하, 모터상수, 모터 드라이버가 낼 수 있는 최대 전류 에 의하여 결정.
- EX) 모터 추력 상수: 10N(\(k_T\) = 10N/A), 모터 드라이버의 최대 전류: 5A 부하의 크기: 1kg
- 마찰력을 무시한 최대허용가속도: \(a_, = \frac{F}{m} = \frac{k_t x i_{max}}{m} = \frac{10x5}{1} = 50m/s^2\)
- EX) 모터 추력 상수: 10N(\(k_T\) = 10N/A), 모터 드라이버의 최대 전류: 5A 부하의 크기: 1kg
최대허용저크
- 최대허용저크의 결정은 다음과 같다.
- 기계적인 강성.
- 시스템의 제어 주파수(인터럽트 주파수)
- 모터 Amplifier의 전류제어 밴드폭
- 모터의 전기적인 시정수(electrical time constant)
- 모터의 공급 전압
- D/A 출력 및 OP amp의 밴드폭
- 10g 이상의 초고속 시스템의 경우 최대 허용저크를 얼마나 높일 수 있느냐에 따라 그 시스템의 운동시간에 대한 성능이 좌우.
최대허용 다이나믹 에러(Endurable Dynamic Error)
- 최소구동시간을 결정짓는 인자를 한가지 더 꼽는다면 구동에 따른 위치오차 를 들 수 있다 = 다이나믹 에러
- 최대로 허용되는 다이나믹 에러는 전체 시스템의 허용오차를 결정짓기 때문에 모듈별 사양(specification)에도 영향을 미친다.
최소구동시간에서 최대허용속도, 가속도가 가장 중요하며 일반적. 최대 허용저크와 최대 허용에러는 시스템의 성능에 따라 경험적으로 결정.
2차 구동프로파일(사다리꼴 속도프로파일) 예제
- 최대허용속도, 최대허용가속도 계산해보고, 트래킹 제어에 활용되는 2차 구동 프로파일을 실제로 생성하고 최소구동시간을 계산
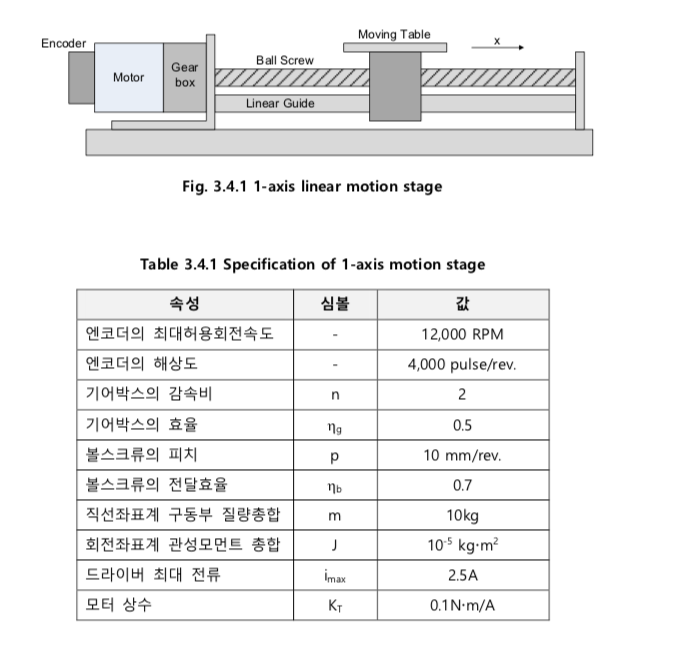
시스템의 구동 제약조건 계산
- 최대허용속도계산
- 엔코더 최대회전수: 12,000RPM, 감속기 통과: 6,000RPM(초당회전수 100RPS(Revolution per second))
- 최대허용속도: 피치(100mm/rev)를 곱하면 1m/s
- 엔코더 최대회전수: 12,000RPM, 감속기 통과: 6,000RPM(초당회전수 100RPS(Revolution per second))
- 엔코더 신호출력의 최대 주파수
- \(f_{max}\) = 200\((\frac{rev.}{s}) \cdot 4,000 (\frac{pulse}{rev.})\) = 800kHz
- 따라서 상기 1축 스테이지가 1m/s의 최대속도를 가지려면, 카운터가 내장되어 있는 DSP나 FPGA는 4체배 기능을 동작할 수 있도록 3.2MHz 이상의 작동주파수 를 가져야함(실제로는 설계마진이 추가)
- 최대허용가속도계산
- 먼저 기어박스의 출력 축에서의 최대 토크:
- \(\tau_{gm} = K_T \cdot i_{max} \cdot n \cdot \eta_g\) = 0.1 x 2.5 x 2 x 0.5 = 0.25 \(N \dot m\)
- 회전- 직선 변환 계수 \(\frac{2\pi}{p}\)를 사용하여 (\(\tau x 2 \pi = F x pitch\)) 직선 좌표계에서의 최대 힘:
- \[F_{max} = \frac{2 \pi \dot \tau_{gm} \eta_b}{p} \approx 110.0N\]
- 여기서, 리니어 가이드 및 볼 스크류의 예압에 따른 마찰에 의한 직선 힘 손실이 약 10N이라고 가정하면, 순수하게 가속에 사용할 수 있는 최대 힘은 약 100N이 된다(회전관성모멘트무시)
- \[A_{max} = \frac{F_m}{m} = \frac{100N}{10kg} = 10m/s^2 \approx 1g\]
- 먼저 기어박스의 출력 축에서의 최대 토크:
- 따라서, 위에서 구한 사항을 정리하면 상기 시스템의 하드웨어 한계치는 다음과 같이 정리:

총 구동거리는 속도 프로파일을 적분한 값이므로, 구동하고자 하는 거리에 따라 등속 구간이 생성될수도 있고, 그렇지 않을 수도 있다.
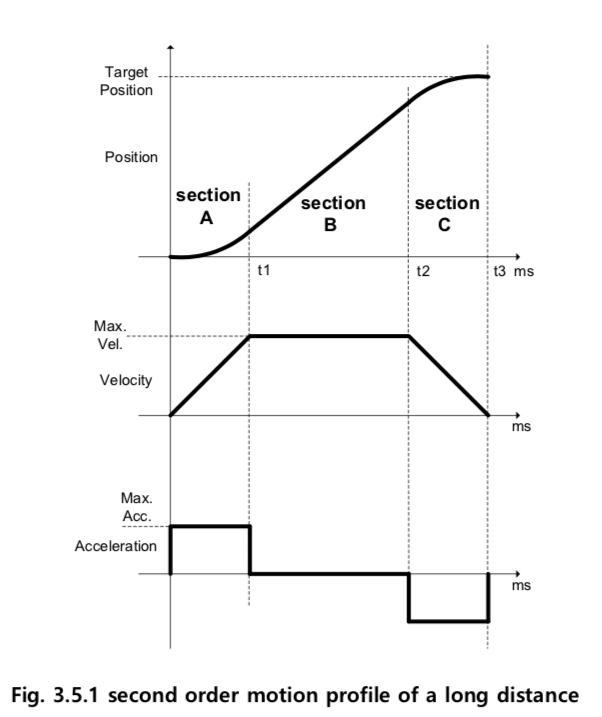
긴 거리의 구동 ( 등속구간이 생기는 경우 , S = 0.5m)
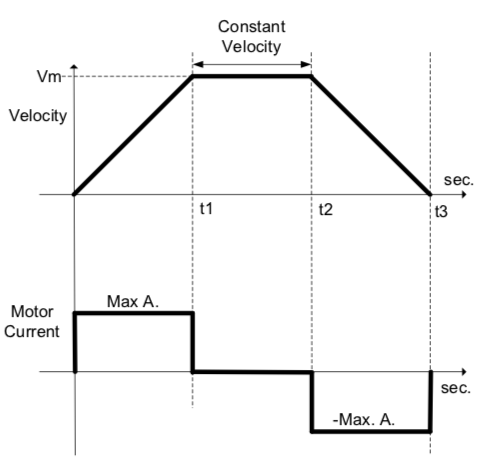
- 구동 시작점(0초)에서 \(t_1\)초까지는 최대 허용 가속도로 가속 (모터에 Max. Ampere(2.5A) 사용).
- \(t_1\) 초부터 \(t_2\) 까지는 최대허용속도로 등속운동
다시 \(t_2\) 초부터 \(t_3\) 까지는 감속 (모터에 Max. Ampere(2.5A) 사용).
- 각 구간의 시간 \(t_1, t_2, t_3\) 등을 수식을 사용하여 계산
- \[t_1 = \frac{V_m}{A_m}\]
- \[t_2 = \frac{s-A_m t^2_1}{V_m} + t_1\]
- \[t_3 = t_2 + t_1\]
하단 그림은 모터에 흘려 주어야 하는 전류 를 도시, 마찰력을 무시하면 모션 프로파일의 가속도 선도와 모터에 흘려주어야 하는 전류의 프로파일은 일치하므로 모션 프로파일의 가속도 선도는 해당 시스템의 전류 제어기의 성능에 상당한 영향
- 여기서 위치프로파일은 가속, 등속, 감속 각 구간별로 속도프로파일을 적분하면 쉽게 얻을 수 있다.
짧은 거리의 구동 ( 등속구간이 생기는 경우 , S = 0.025m)
- 최대허용가속도로 가속을 하여도 Fig.3.4.4과 같이 최대허용속도에 도달하기 전에 감속구간에 진입
- 따라서, 등속구간이 형성되지 않음.
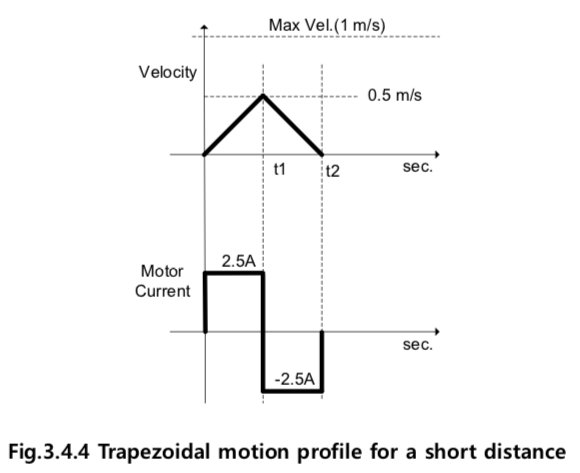
- 등속구간이 없으므로 전체 구동시간의 절반동안 가고자 하는 거리의 절반을 구동.
구동해야 하는 거리가 주어지면, 먼저 등속구동구간이 생기는지 안 생기는지를 계산
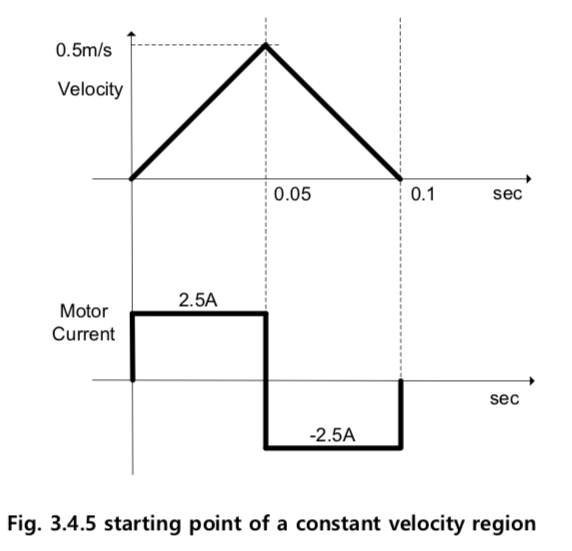
- 등속구간이 형성되기 시작하는 거리 \(S_c\): 가속구간에서 최대가속도로 가속하여 최대속도에 도달하자마자 감속했을때 구동하는 거리
- \[S_c = 0.5 \cdot A_m \cdot (\frac{V_m}{A_m})^2 \cdot 2\]
- 등속구동구간이 생기기 시작하는 거리 \(S_c\)에서의 \(t_1, t_2\)를 구해보면
- \[t_1 = \frac{V_m}{A_m}\]
- \[t_2 = 2 t_1\]
- 실제 모터의 구동을 위해서는 상기에서 설명한 프로세스를 프로그램화해서 제어기에 삽입해야하므로 알고리즘의 동작 순서를 정리하면 다음과 같다
- 구동거리를 결정(혹은 상위제어기에서 받는다).
- 구동해야하는 거리 S와 등속구간이 형성되는 거리 \(S_c\)를 비교하여 등속구간의 형성여부를 체크.
- 등속구간이 없는 경우 가속시간 \(t_1\) 및 최종구동시간 \(t_2\)를 구함.
- 등속구간이 있는 경우 가속시간 \(t_1\), 감속시작시간 \(t_2\) 및 최종구동시간 \(t_3\)를 구함.
- 모션을 시작하면서 매 인터럽트 시간마다 상기 프로파일의 수식을 사용하여 목표 위치 점을 계산하면서 이를 이용하여 구동.
사다리꼴 속도기반의 2차 구동프로파일 계산
- 이전에 계산 했던 프로세스를 S/W 알고리즘으로 변환하기 쉽도록 수식을 사용하여 구체적으로 정리
Reference: