Robot Dynamics & control: Lecture 5 - Velocity Kinematics - The Manipulator Jacobian
in Robotics / Robotics & Control on Robotics
Table of Contents
- Introduction
- Angular Velocity: The Fixed Axis Case
- Skew Symmetrix Matrices
- Angular Velocity: The General Case
- Addition of Angular Velocities
- The General I.K. Problem
- Kinematic Decoupling
- Inverse Position: A Geometric Approach
- Inverse Orientation
- Inverse Kinematics: A Numerical Approach
Introduction
- In this chapter, we derive the velocity relationships, relating the linear and angular velocities of the end-effector(or any other point on the manipulator) to the joint velocities.
- Mathematically, the forward kinematic equations define a function between the space of Cartesian position and orientations and the space of joint positions.
- The velocity relationships are then determined by the Jacobian of this function
- Jacobian matrix: one of the most important quantities in robotic manipulation
- In the planning and exectution of smooth trajectories, in the determination of singular configurations, in the execution of coordinated anthropomorphic motion, and in the transformation of forces and torques from the end-effector to the manipulator joints.
Angular Velocity: The Fixed Axis Case
When a rigid body moves in a pure rotation about a fixed axis, every point of the body moves in a circle. If k is a unit vector in the direction of the axis of rotation, then the angular velocity is given by \[\begin{aligned} \omega = \dot{\theta} k \end{aligned}\]
Given the angular velocity of the body, the linear velocity of any point of the body is given by \[\begin{aligned} v = \omega \dot r \end{aligned}\]
- \(v\): Linear velocity of a point
- \(\omega\): Angular velocity of a point
- \(r\): A vector from origin which is lie on the axis of rotation
Generally, the main role of an angular velocity is to induce linear velocities of points in a rigid body, but here we are interested in describing the motion of moving frame, including the motion of the origin of the frame and the rotational motion of the frame’s axes.
Skew Symmetrix Matrices
When the axis of rotation is not fixed, or when the angular velocity is the result of multiple rotations about distinct axes, it it necessary to develop a more general representation for angular velocities.
Skew symmetric matrix is required to simplify the relative velocity transformtions between coordinate frames.
Definition 5.1 A matrix S is said to be skew symmetrix if and only if \[\begin{aligned} S^T + S = 0 \end{aligned}\]
We denote the set of all 3 x 3 skew symmetric matrices by SS(3).
If \(S\in SS(3)\), \[\begin{aligned} s_{ij} + s_{ji} = 0 \quad i, j = 1, 2, 3 \end{aligned}\]
Thus, \[\begin{aligned} S = \begin{bmatrix} 0 & -s_3 & s_2\\ s_3 & 0 & -s_2\\ -s_2 & s_1 & 0\\ \end{bmatrix} \end{aligned}\]
If \(a = (a_x, a_y, a_z)^T\) is a 3- vector, we define the skew symmetric matrix S(a) as \[\begin{aligned} S = \begin{bmatrix} 0 & -s_z & s_y\\ s_z & 0 & -s_x\\ -s_y & s_x & 0\\ \end{bmatrix} \end{aligned}\]
Ex. 5.1 We denote by i, j and k the 3 unit basis coordinate vectors, \[\begin{aligned} \hat{i} = \begin{bmatrix} 1 \\ 0 \\ 0\\ \end{bmatrix} \quad \hat{j} = \begin{bmatrix} 0 \\ 1\\ 0\\ \end{bmatrix} \quad \hat{k} = \begin{bmatrix} 0 \\ 0 \\ 1\\ \end{bmatrix} \end{aligned}\]
Then \[\begin{aligned} S(\hat{i}) = \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0\\ \end{bmatrix} \quad S(\hat{j}) = \begin{bmatrix} 0 & 0 & 1\\ 0 & 0 & 0\\ -1 & 0 & 0\\ \end{bmatrix} \quad S(\hat{k}) = \begin{bmatrix} 0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0\\ \end{bmatrix} \end{aligned}\]
Property of Skew Symmetric Matrices
- 1) The operator S is linear,
- For nay vectors \(a\) and \(b\) belonging to \(R^3\) and scalar \(\alpha, \beta\)
- 2) For any vectors \(a\) and \(p\) belonging to \(R^3\)
- where \(a\) x \(p\) denotes the vector cross product
- 3) For \(R \in SO(3)\) and a,b \(\in R^3\)
- Below Eq. is not true in general unless R is orthogonal
- 4) For \(R \in SO(3)\) and a \(\in R^3\)
- This property follow easily from 2) and 3). Let \(b \in R^3\) be an arbitrary vector them
- 5) For an n x n skew symmetric matrix S and any vector \(X \in R^n\)
The derivative of a Rotation Matrix
Suppose \(R = R(\theta) \in SO(3)\) for every \(\theta\) . \[\begin{aligned} R(\theta) R(\theta)^T = I \end{aligned}\]
Differentiating both sides with respect to \(\theta\) \[\begin{aligned} \frac{dR}{d\theta} R(\theta)^T + R(\theta) \frac{dR^T}{d\theta} = 0 \end{aligned}\]
Let us define the matrix S as $$
\begin{aligned} S = \frac{dR}{d\theta} R(\theta)^T \end{aligned} $$
Then the transpose of S is \[\begin{aligned} S^T = (\frac{dR}{d\theta} R(\theta)^T)^T = R(\theta) \frac{dR^T}{d\theta} \end{aligned}\]
Therefore(\(\because S + S^T = 0\)), \[\begin{aligned} \frac{dR}{d\theta} R(\theta)^T + R(\theta) \frac{dR^T}{d\theta} = 0 \end{aligned}\]
This means that the matrix S defined above is skew symmetric.
Multiplying both sides on the right by R and using the fact that \(R^TR =I\) yields for \(S = \frac{dR}{d\theta} R(\theta)^T\) \[\begin{aligned} \frac{dR}{d\theta} = S R(\theta) \end{aligned}\]
The above Eq. is very important. It says that computing the derivative of the rotation matrix R is equivalent to a matrix multiplication by a skew symmetric matrix S.
Angular Velocity: The General Case
- We now consider the general case of angular velocity about an arbitrary possibly moving, axis.
- Suppose that R is time-varying, so that \(R = R(t) \in SO(3)\) for every \(t \in R\)
- Assuming that R(t) is continuously differentiable as a function of t,
Relationship between angular velocity and the derivative of a Rotation matrix
where the matrix \(S(\omega(t))\) is skew symmetrix.
- \(\omega(t)\) : Angular velocity of the rotating frame w.r.t the fixed frame at time t.
Consider a point \(p\) rigidly attached to a moving frame. The coordinates of p relative to the fixed frame are given by \(p^0 = R^0_1 p^1\) \[\begin{aligned} \frac{d}{dt} p^0 &= \dot{R^0_1} p^1 \\ &= S(\omega) R^0_1 p^1 \\ &= \omega \times R^0_1 p^1 \\ &= \omega \times p^0 \end{aligned}\]
- \(omega\): traditional angular velocity vector
Addition of Angular Velocities
- We are often interested in findingthe resultant angular velocity due to the relative rotation of several coordinate frames.
- We now derive the expressions for the composition of angular velocities of two frames \(o_1 x_1 y_1 z_1\) and \(o_2 x_2 y_2 z_2\) relative to the fixed frame \(o_0 x_0 y_0 z_0\).
- The 3 frames share a common origin.
- This chapter is concerned with the inverse problem of finding the joint variables in terms of the end-effector position and orientation.
- After formulating the general I.K probelm, we study the principle of kinematic coupling that simplifies the I.K. by decoupling the position and orientation.
- We describe a geometric approach for solving the position problem, while we exploit the Euler angle parameterizaiton to solve the orientation problem.
The General I.K. Problem
\[\begin{aligned} H = (x, y , z, \psi, \theta , \phi) = \begin{bmatrix} R & o \\ 0 & 1 \\ \end{bmatrix} \in SE(3) \end{aligned}\]with \(R \in SO(3)\), find (one or all) solutions of the equation \[\begin{aligned} T ^0 _n (q_1, \cdots, q_n) = H \end{aligned}\]
where \[\begin{aligned} T ^0 _n (q_1, \cdots, q_n) = A_1(q_1) \cdots A_n(q_n). \end{aligned}\]
\[\begin{aligned} T ^0 _n (q_1, \cdots, q_n) &= H \\ \begin{bmatrix} T_{11} & T_{12} & T_{13} & T_{14}\\ T_{21} & T_{22} & T_{23} & T_{24} \\ T_{31} & T_{32} & T_{33} & T_{34} \\ T_{41} & T_{42} & T_{43} & T_{44} \\ \end{bmatrix} &= \begin{bmatrix} c_{\phi}c_{\theta} & -s_{\phi}c_{\psi}+c_{\phi}s_{\theta}s_{\psi} & s_{\phi}s_{\psi} + c_{\phi}s_{\theta}c_{\psi} & x\\ s_{\phi}c_{\theta} & c_{\phi}c_{\psi}+s_{\phi}s_{\theta}s_{\psi} & -c_{\phi}s_{\psi} + s_{\phi}s_{\theta}c_{\psi} & y\\ -s_{\theta} & c_{\theta}s_{\psi} & c_{\theta}c_{\psi} & z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{aligned}\]Our task is to find the values for the joint variables \(q_1, ..., q_n\) so that \(T^0_n (q_1, ..., q_n) = H\)
- Given matrix: H, roll/pitch/yaw rotation w.r.t inertial frame
\(\rightarrow\) translation w.r.t inertial frame frame \(\rightarrow\) roll/pitch/yaw rotation w.r.t current frame.
- The above equation results in 12 nonlinear equations in n unknown variables, which can be written as
where \(T_{ij}, h_{ij}\) refer to the 12 nontrivial entries of \(T^0_n\) and \(H\).
Example
- Recall the Stanford manipualtor.
- Suppose that the desired position and orientation of the final frame are given by

- To find the corresponding variables \(\theta_1, ..., \theta_6\), we must solve the following simultaneous set of nonlinear trigonometric eq.
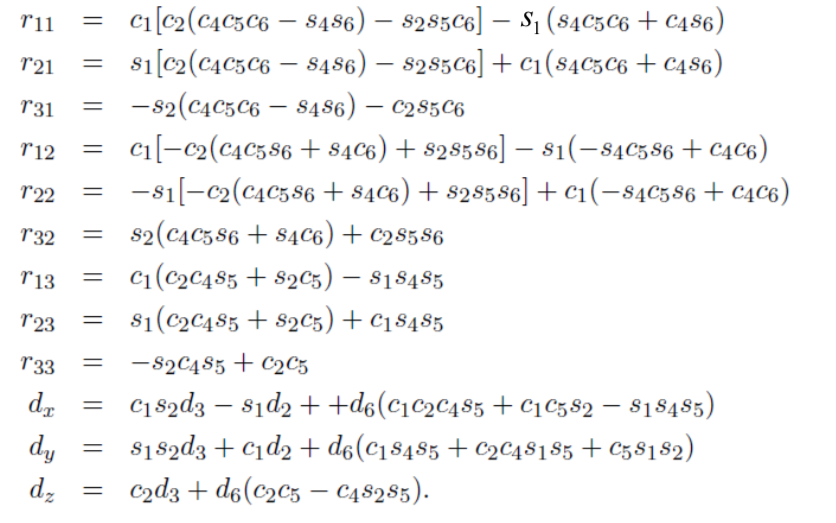
Note
It is too difficult to solve directly in closed form.
Therefore, it is necessary to develop efficient and systematic techniques.
The inverse kinematics problem may or may not have a solution.
Even if a solution exist, it may or may not be unique.
- Inverse kinematics solution:
- A closed form solution
- A numerical solution
- A closed form solution means following explicit relationship
- Advantages of closed form solution.
- Closed form solution is more accurate and faster than numerical solution.
- Closed form solution allows one to develop rules for choosing a particular solution among several multiple solutions.
- It means that you can get the desired pose by selecting the sign, numerical method is impossible.
Kinematic Decoupling
- For manipulators having 6 joints with the last three joint intersecting at a point, it is possible to decouple the I.K. problem into two simper problems;
- Inverse position kinematics
- Inverse orientation kinematics
- Let us suppose that there are exactly 6 degrees-of-freedom and that the last 3 joint axes intersect at a point \(o_c\).
\(o\) and \(R\) are desired position and orientation of the tool frame with respect to the world coordinate system.
- Assumption: axes \(z_3, z_4\), and \(z_5\) intersect at \(o_c\) and hence the origins \(o_3, o_4\) and \(o_5\) will be at the wrist center \(o_c\).
- Motion of final 3 links about these axes will not change the position of \(o_c\)
- Thus, the position of the wrist center is thus function of only the first 3 joint variables (\(\thata_1, \theta_2\) and \(d_3\)).
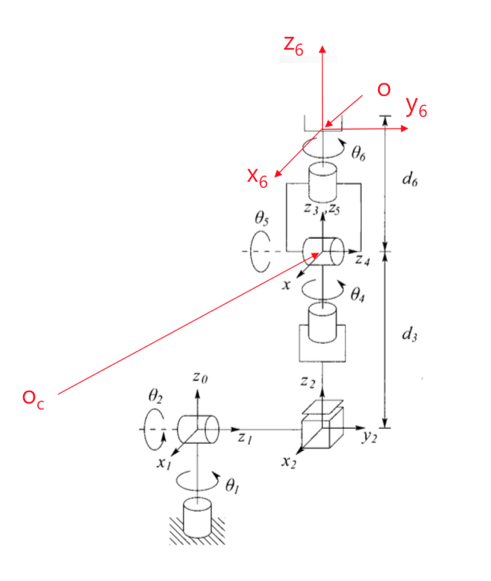
- The origin of the tool frame, \(o\):
\[\begin{aligned} \begin{bmatrix} x_c\\ y_c\\ z_c\\ \end{bmatrix} = \begin{bmatrix} o_x - d_6 r_{13}\\ o_y - d_6 r_{23} \\ o_z - d_6 r_{33} \\ \end{bmatrix} \quad where \quad R = \begin{bmatrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33}\\ \end{bmatrix} \end{aligned}\]Third columns of \(R^0_6\) and \(R^0_5\) are the same!
By using the above eq., we may find the values of the first 3 joint variables.
This determines the orientation transformation \(R^0_3\) which depends only on these first 3 joint variables.
- Orientation of the end-effector relative to the frame \(o_3 x_3 y_3 z_3\)
- \(R\): given
- \(R^0_3\): can be calculated once the first 3 joint variables are known.
- \(R^3_6\): unknown
Then, the final 3 joint variables can be found as a set of Euler angles corresponding to \(R^3_6\).
- Summary
- For this class of manipulators the determination of the I.K. can be summarized by the following algorithm.
Step 1: Find \(q_1, q_2, q_3\) such that the wrist center \(o_c\) has coordinates given by \[\begin{aligned} o^0_c &= o - R^0_5 \begin{bmatrix} 0\\ 0 \\ d_6\\ \end{bmatrix} = o - R \begin{bmatrix} 0\\ 0 \\ d_6\\ \end{bmatrix} \end{aligned}\]
Step 2: Using the joint variables determined in Step 1, evaluate \(R^0_3\).
Step 3: Find a set of Euler angles corresponding to the rotation matrix \[\begin{aligned} & R^3_6 = (R^0_3)^{-1} R = (R^0_3)^T R . \end{aligned}\]
Inverse Position: A Geometric Approach
- We can use a geometic approach to find the variables \(q_1, q_2, q_3\) corresponding to \(o^0_c\).
- Two reasons for the geometric approach:
- Most manipulator designs are kinematically simple (without joint offset), usually consisting of 1 of the 5 basic configurations with a spherical wrist.
- There are few techniques that can handle the general I.K. problem for arbitrary configurations.
- The general idea of the geometric approach is to solve for joint variable \(q_i\) by projecting the manipulator onto the \(x_{i-1} - y_{i-1}\) plane and solving a simple trigonometry problem.
Articulated Configuration
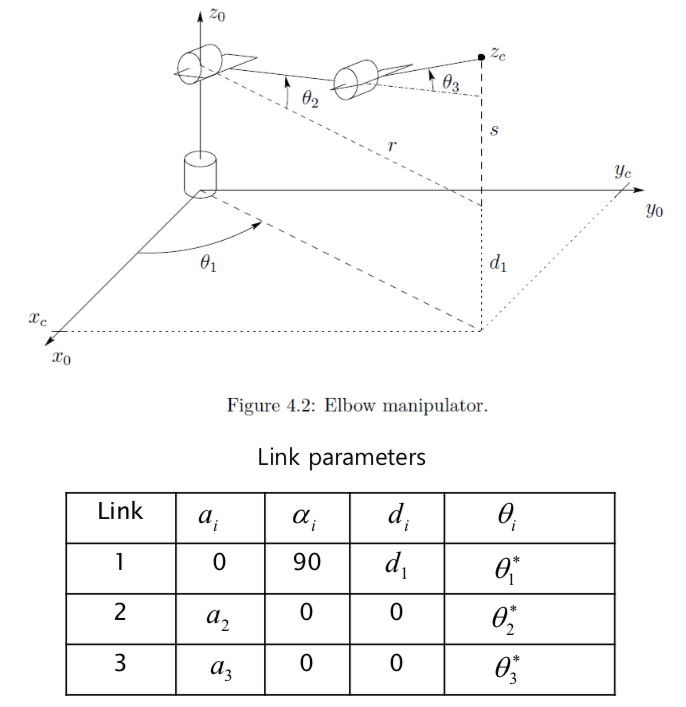
Consider the elbow manipulator shown in Fig. 4.2, with the components of denoted \(o^0_c\) by \(x_c, y_c, z_c\). We project \(o_c\) onto the \(x_0 - y_0\) plane.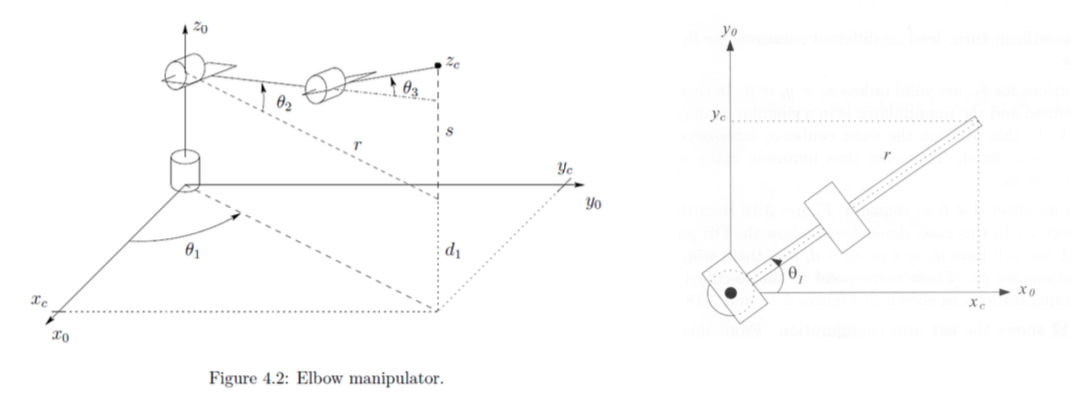
From this projection \[\begin{aligned} \theta_1 = Atan2 (y_c, x_c) \end{aligned}\]
Note that a second valid solution for \(\theta_1\) is \[\begin{aligned} \theta_1 = \pi + Atan2 (y_c, x_c) \end{aligned}\]
This second solution leads to different solutions for \(\theta_2\) and \(\theta_3\).
The above solution is valid unless \(x_c = y_c = 0\). In this case, the manipulator is in a singular configuration shown in Fig. 4.5, and there are thus infinitely many solutions for \(\theta_1\).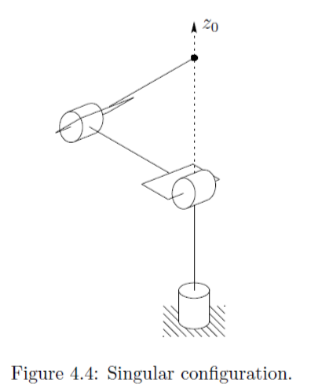
If there is an offset d, then the wrist center cannot intersect \(z_0\). In this case, there will be only 2 solution for \(\theta_1 \rightarrow\) These correspond to the so-called left arm and right arm configuration.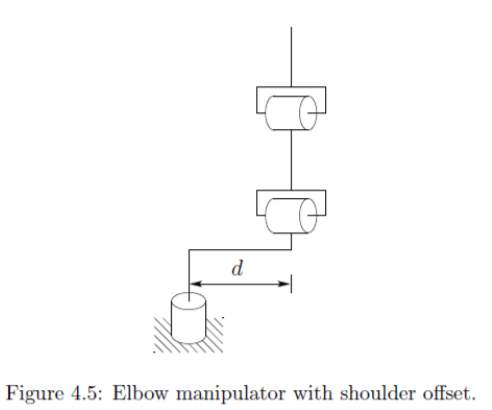
- Case 1) Left arm configuration:
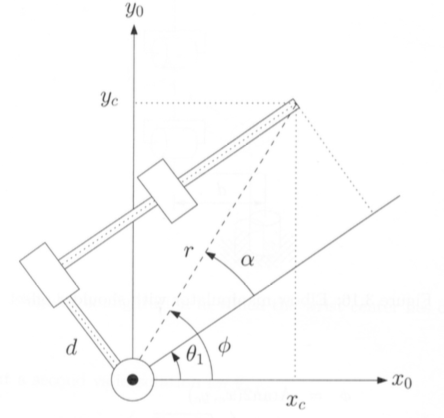
Geometrically, \[\begin{aligned} & \theta_1 = \phi - \alpha \\ & where, \phi = Atan2(y_c, x_c), \alpha = Atan2(d, \sqrt{r^2 - d^2}) = Atan2(d, \sqrt{x_c^2 + y^2_c -d^2}) \end{aligned}\]
- Case 2) Right arm configuration:
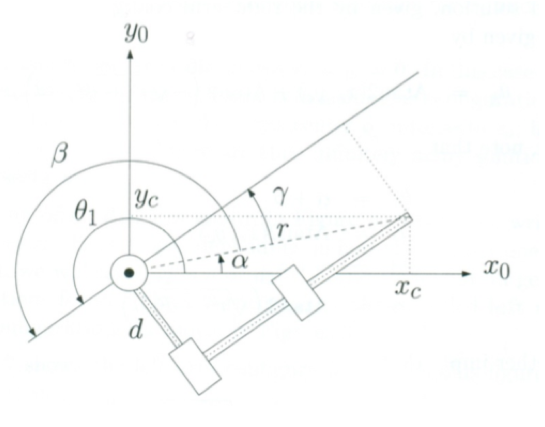
Geometrically, \[\begin{aligned} & \theta_1 = \alpha + \beta \\ where, \alpha &= Atan2(y_c, x_c), \beta = \gamma + \pi = Atan2(d, \sqrt{r^2 - d^2}) + \pi = Atan2(- d, - \sqrt{r^2 + -d^2}) \end{aligned}\]
- To find the \(\theta_2, \theta_3\):
To find the angles \(\theta_2, \theta_3\) for the elbow manipulator given \(\theta_1\), we consider the plane formed by the second and third links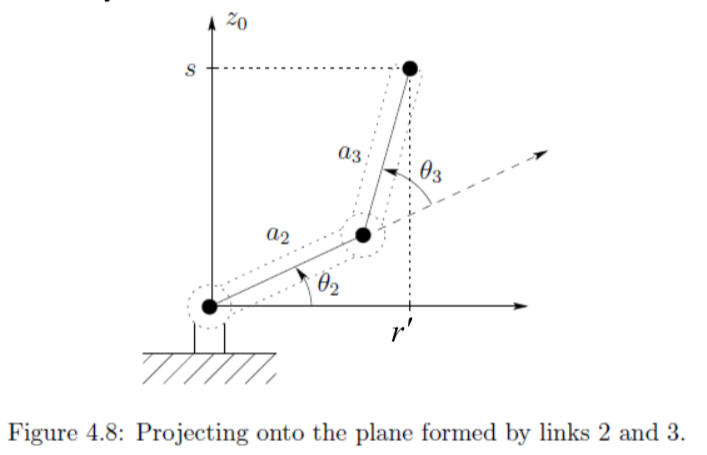
Previously, \[\begin{aligned} & \theta_3 = Atan2(\pm \sqrt{1-D^2}, D) \\ where, D &= cos\theta_3 = \frac{r'^2 + s^2 -a ^2_2 -a^2_3}{2a_2 a_3} = \frac{(x^2_c + y^2_c -d^2) + (z_c -d_1)^2 -a ^2_2 -a^2_3}{2a_2 a_3} \end{aligned}\]
Similarly, \[\begin{aligned} \theta_2 &= Atan2(s, r') - Atan2(a_3s_3, a_2 +a_3c_3) \\ &= Atan2(z_c -d_1, \sqrt{x^2_c + y^2_c -d ^2}) - Atan2(a_3s_3, a_2 + a_3c_3) \end{aligned}\]
The two solution for \(\theta_3\) correspond to the elbow-up position and elbow-down position, respectively.

Spherical Configuration
we solve the inverse position kinematics for a 3 D.O.F spherical manipulator. The first joint variable is the base rotation and solution is \[\begin{aligned} \theta_1 = Atan2(y_c, x_c) \qquad x_c \neq 0 \quad and \quad y_c \neq 0 \end{aligned}\]
Second solution is \[\begin{aligned} \theta_2 = \pi + Atan2(y_c, x_c) \end{aligned}\]
if both \(x_c\) and \(y_c\) are zero, the configuration is singular and \(\theta_1\) may take on any value.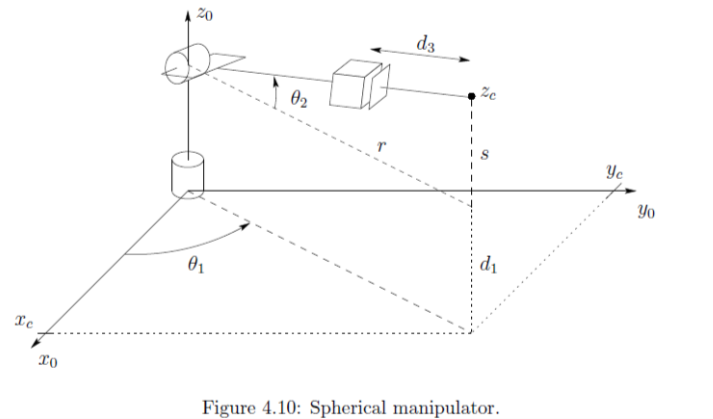
The angle \(\theta_2\) is given by \[\begin{aligned} \theta_2 = Atan2(s, r) \end{aligned}\]
where \(r^2 = x^2_c + y^2 _c, s = z_c - d_1\)
The linear distance \(d_3\) is found as \[\begin{aligned} d_3 = \sqrt{r^2 + s^2} = \sqrt{x^2_c + y^2_c + (z_c - d_1)^2} \end{aligned}\]
There are 2 solutions to the inverse position kinematics as long as the wrist center does not intersect \(z_0(x_c, y_c \neq 0)\).
If there is an offset them there will be left and right arm configurations.
Inverse Orientation
- The inverse position problem gives the values of the first 3 joint variables corresponding to a given position of the wrist center.
- The inverse orientation problem is finding the values of the final 3 joint variables corresponding to a given orientation with respect to the frame \(o_3 x_3 y_3 z_3\).
- The inverse orientation problem can be interpreted as the problem of finding a set of Euler angles corresponding to a given rotation matrix R.
- Recall that the rotation matrix obtained for the spherical wrist has the same form as rotation matrix for the Euler transformation:
Even they have different forms, we can easily find the joint angles.
Example1: Articulated Manipulator with Spherical Wrist
Using DH parameters, we can derive the matrix \(R^0_3\). \[\begin{aligned} R^0_3 = &= \begin{bmatrix} R^3_6 & o^3_6\\ 0 & 1\\ \end{bmatrix} &= \begin{bmatrix} c_1 c_{23}& - c_1 s_{23} & s_1 \\ s_1 c_{23} & -s_1 s_{23} & -c_1\\ s_{23} & c_{23} & 0 \\ \end{bmatrix} \end{aligned}\]
The matrix \(R^3_6\) is the upper left 3x3 submatrix of the matrix product \(A_4A_5A_6\) given by \[\begin{aligned} R^3_6 &= \begin{bmatrix} c_4 c_5 c_6 - s_4 s_6& -c_4 c_5 s_6 -s_4 c_6 & c_4 s_5 \\ s_4 c_5 c_6 + c_4s_6 & -s_4 c_5 s_6 + c_4 c_6 & s_4 s_5 \\ -s_5 c_6 & s_5 s_6 & c_5 \\ \end{bmatrix} \end{aligned}\]
The equation to be solved for the final 3 variables is therefore
- \(R\): given
Third column comparison: \[\begin{aligned} & c_4 s_5 = c_1 c_{23} r_{13} + s_1 c_{23} r_{23} + s_{23} r_{33} \\ & s_4 s_5 = -c_1 s_{23} r_{13} -s_1 s_{23} r_{23} + c_{23} r_{33} \\ & c_5 = s_1 r_{13} - c_1 r_{23}\\ & \therefore \theta_5 = Atan2(\pm \sqrt{1-(s_1 r_{13} - c_1 r_{23})^2 , s_1 r_{13} - c_1 r_{23}}) \end{aligned}\]
If the positive square root is choosen, \[\begin{aligned} & \theta_4 = Atan2(s_4 s_5, c_4 s_5) \\ & \theta_4 = Atan2((-c_1 s_{23} r_{13} -s_1 s_{23} r_{23} + c_{23} r_{33}) , (c_1 c_{23} r_{13} + s_1 c_{23} r_{23} + s_{23} r_{33}) ) \\ \end{aligned}\]
Third row comparison: \[\begin{aligned} & -s_5 c_6 = s_1 r_{11} - c_1 r_{21} \\ & s_5 s_6 = s_1 r_{12} - c_1 r_{22} \\ & \theta_6 = Atan2( s_5 s_6 , -(-s_5 c_6)\\ & \therefore \theta_6 = Atan2(( s_1 r_{12} - c_1 r_{22}) , (-s_1 r_{11} + c_1 r_{21})) \end{aligned}\]
If the negative square root is choosen, \[\begin{aligned} & \theta_4 = Atan2(-s_4 s_5, -c_4 s_5) \\ & \theta_4 = Atan2((c_1 s_{23} r_{13} + s_1 s_{23} r_{23} - c_{23} r_{33}) , (-c_1 c_{23} r_{13} - s_1 c_{23} r_{23} - s_{23} r_{33}) ) \\ & \theta_6 = Atan2( -s_5 s_6 , (-s_5 c_6)\\ & \theta_6 = Atan2(( -s_1 r_{12} + c_1 r_{22}) , (s_1 r_{11} - c_1 r_{21})) \end{aligned}\]
If \(s_5 = 0\), then joint axes \(z_3\) and \(z_5\) are colinear, and this is a singular configuration, so there are infinitely many solution($$\theta_4 + \theta_6 can be determined)
Example2: Articulated Manipulator with Spherical Wrist
One complete inverse kinematic solution of the 6 DOF elbow manipulator which has no joint offsets and a spherical wrist.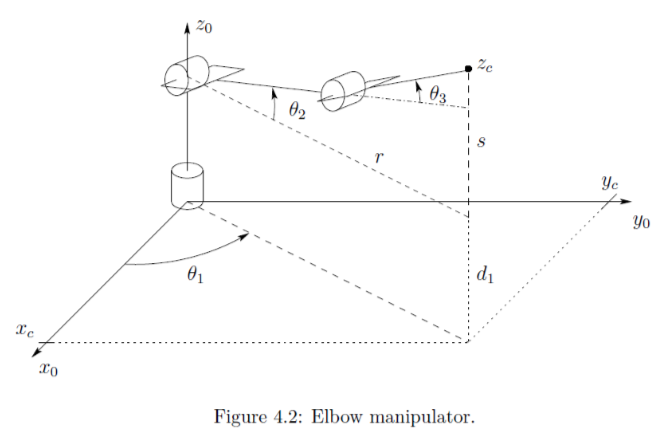
Given,
- \(o\): end-effector position
- \(R\): end-effector orientation
then, wrist center: \[\begin{aligned} & x_c = o_x - d_6 r_{13}\\ & y_c = o_y - d_6 r_{23}\\ & z_c = o_z - d_6 r_{13}\\ \\ & \theta_1 = Atan2(y_c, x_c)\\ & \theta_2 = Atan2(z_c -d_1, \sqrt{x^2_c +y^2_c}) - Atan2(a_3 s_3, a_2 + a_3c_3) \\ & \theta_3 = Atan2(\pm \sqrt{1-D^2}, D) \\ & \qquad where,\quad D = \frac{x^2_c + y^2_c + (z_c -d_1)^2 - a_2 ^2 - a^2 _3}{2 a_2 a_3} \\ & \theta_4 = Atan2(\pm (-c_1s_{23}r_{13} -s_1s_{23}r_{23} + c_{23}r_{33}), \pm (c_1c_{23}r_{13} + s_1 c_{23} r_{23} + s_{23} r_{23}))\\ & \theta_5 = Atan2(\pm \sqrt{1-(s_1 r_{13} - c_1 r_{23})^2}, s_1 r_{13} -c_1 r_{23})\\ & \theta_6 = Atan2(\pm (s_1 r_{12 - c_1 r_{22}}), \pm (-s_1 r_{11} + c_1 r_{21}))\\ \end{aligned}\]
Example3: SCARA Manipulator
Forward kinematics defined by
There is no solution of the above equation, unless R is of the form \[\begin{aligned} R = \begin{bmatrix} c_\alpha & s_\alpha & 0 \\ s_\alpha & -c_\alpha & 0\\ 0 & 0 & -1 \\ \end{bmatrix} \\ \end{aligned}\]
And if this is the case, the sum $$\theta_1 + \theta_2 - \theta_4 is determined by \[\begin{aligned} \theta_1 + \theta_2 - \theta_2 = \alpha = Atan2(r_{12}, r_{11}) \end{aligned}\]
Projecting the manipulator configuration onto the \(x_0 - y_0\) plane: \[\begin{aligned} & \theta_2 = Atan2(\pm \sqrt{1-c^2_c}, c_2)\\ &where \quad c_2 = \frac{x_c^2 +y^2_c -a_1^2 -a^2_2}{2a_1a_2}\\ & \theta_1 = Atan2(y_c, x_c) - Atan2(a_2s_2, a_1 + a_2 c_2) \end{aligned}\]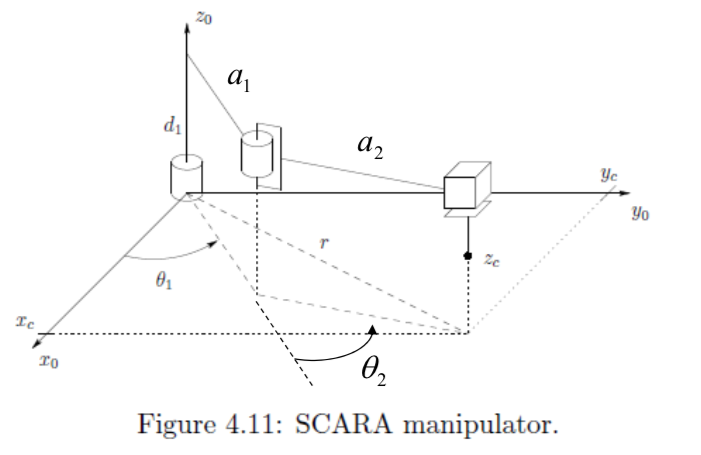
Then, \[\begin{aligned} \theta_2 &= \theta_1 + \theta_2 - \alpha \\ &= \theta_1 + \theta_2 -Atan2(r_{12}, r_{11}) \end{aligned}\]
Finally, \[\begin{aligned} d_3 = - o_z - d_4 \end{aligned}\]
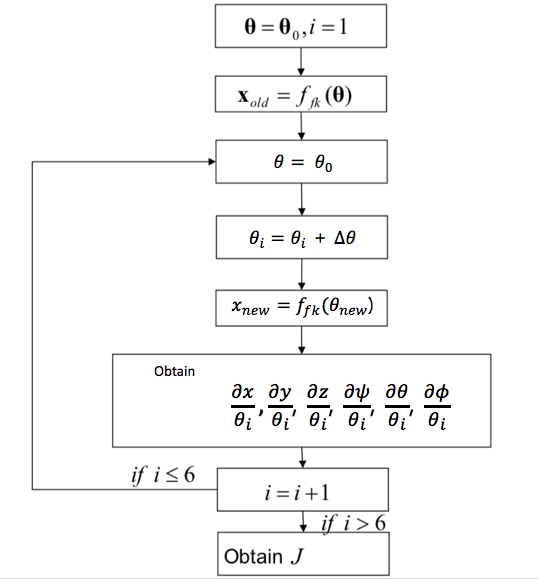
Inverse Kinematics: A Numerical Approach
- Basic flowchart:
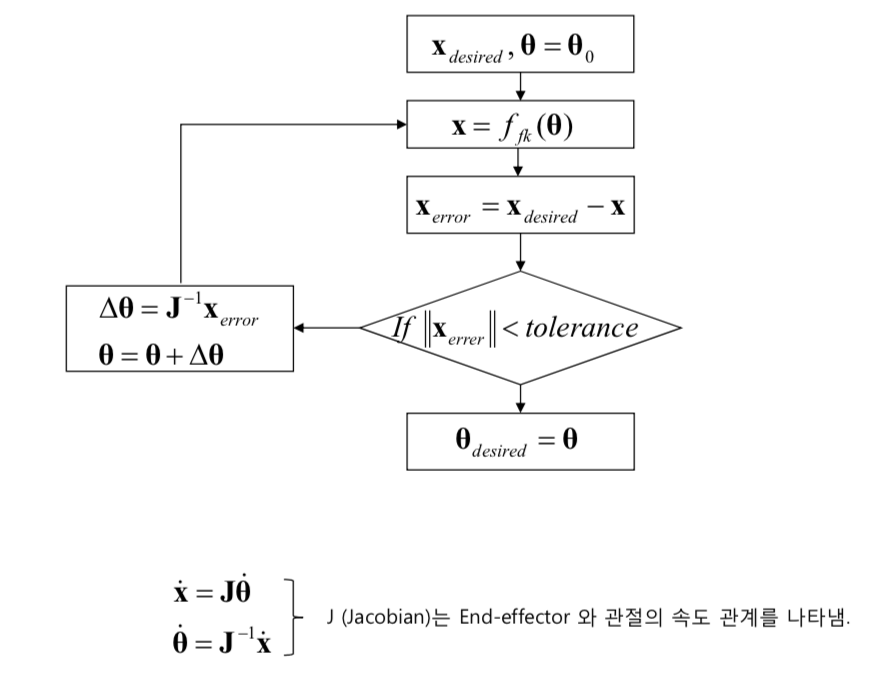
- Numerical derivation of J:

Reference: